Условия сходимости ряда Фурье

Знак равенства ставить в формуле (9) преждевременно, так как способ получения его коэффициентов был нестрогим, а ряд Фурье функции может и расходиться.

 

Т. Дирихле.( достаточные условия сходимости ряда Фурье)

Пусть -периодическая функция удовлетворяет двум условиям:

1. кусочно-непрерывна на отрезке ;

2. кусочно-монотонна на отрезке .

Тогда соответствующий функцииряд Фурье сходится на этом отрезке и при этом:

1) в точках непрерывности функции сумма ряда совпадает с самой функцией, т.е. ;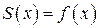

2) в каждой точке разрыва функции сумма ряда равна среднему арифметическому пределов функции слева и справа, т.е.

; (10)

3) в точках и (на концах отрезка) сумма ряда равна:

. (11)

 

Условия1 и2 называются условиями Дирихле. Таким образом, если функция удовлетворяет условиям Дирихле, то на отрезке имеет место разложение:

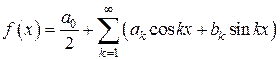, (12)