ОЦЕНКА ОСТАТКА ЗНАКОЧЕРЕДУЮЩЕГОСЯ РЯДА

Пусть 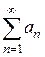– сходящийся числовой ряд. Тогда его сумму можно представить в виде ,
где – -ный остаток ряда.

 

Если , то говорят, что с точностью .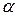

 

Для знакочередующегося ряда по теореме Лейбница . Этот факт используется в приближенных вычислениях.

Пример. Вычислите сумму ряда с точностью .

Решение.

Ряд сходится. .

С заданной точностью

.

Ответ. .

 

В экономике ряды применяются в основном в теоретических исследованиях.

 

Пример.

 

Предположим, что рассматривается задача о рыночной цене бессрочной облигации номиналом 1000$ и 3-% купоном. Это значит, что владелец этой облигации каждый год должен получать 30$. Необходимо определить истинную цену этой бесконечной последовательности платежей.

Любая валюта подвержена инфляции. Если инфляция составляет 2% в год, то 30$, которые получим через год, сейчас равны $, которые планируем получить через 2 года, сейчас равны и т.д. В итоге получаем, что бесконечный ряд платежей в 30$, которые будем получать каждый год, сейчас эквивалентны сумме ряда

.

Применив формулу суммы бесконечно убывающей геометрической прогрессии, получим

.