СХОДИМОСТЬ ПОЛОЖИТЕЛЬНЫХ РЯДОВ

I. Признак сравнения. Если даны два ряда с неотрицательными членами, причём, начиная с некоторого номера n > N все , то

1. если 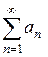– расходящийся ряд, то ряд расходится;

2. если – сходящийся ряд, то ряд сходится.

Для сравнения часто используются ряды:

1. 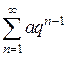(геометрический), сходится при и расходится при .

Доказательство…

2. (обобщённый гармонический ряд), сходится при и расходится при .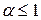

Пример. .

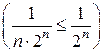Признак сравнения в предельной форме. Даны два ряда с неотрицательными членами. Если существует конечный предел , то ряды (1) и (2) либо оба сходятся, либо расходятся.

Более точно: Если существует конечный предел , то при из сходимости ряда (2) следует сходимость ряда (1), а при 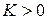из расходимости ряда (1) следует расходимость ряда (2).