Условная вероятность события

Пусть - вероятностное пространство (дискретное) и произвольное событие из 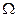, удовлетворяющее условию . Определим на 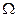функцию следующим образом: .

Легко убедиться, что функция является вероятностью на пространстве 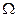. Действительно, первое условие определение вероятности – условие неотрицательности, очевидно, выполняется. Далее, поскольку, то и второе условие определения вероятности у нас выполняется.

Определение 1. Функция называется условной вероятностью на 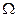, индуцированной событием В.

Определение 2. Условной вероятностью события 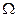относительно события 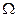называется число .

Основные свойства условной вероятности:

  1. .

Действительно, так как при , то .

  1. .
  2. .

Предположим, что элементарные события равновозможны. Тогда в силу свойства1. . Отсюда следует, что условная вероятность представляет собой вероятность события , вычисленную при дополнительном предположении, что произойдет событие В.

Примет 1. Брошены две игральные кости. Требуется определить вероятность того, что сумма выпавших на них очков равна 8 (событие А), если известно, что эта сумма есть четное число (событие В).

Число всех исходов равно 36. Число исходов, благоприятствующих событию А равно 5. Так как i+j=8 удовлетворяется при i=2, 3, 4, 5, 6 и j=6, 5, 4, 3, 2. Следовательно, вероятность события А равна . Вычислим теперь вероятность . Так как число исходов (i, j) с четной суммой i+j=18, то .

Пример 2. Из колоды карт последовательно вынуты две карты. Найти вероятность того, что вторая карта будет тузом, если первоначально был вынут туз.

Обозначим {первоначально был вынут туз},

{вторая карта является тузом}.

.

Пример 3. Вероятность попасть в самолет равна 0,4, а вероятность его сбить равна 0,1. Найти вероятность того, что при попадении в самолет он будет сбит.

Обозначим {попадение в самолет},

{самолет сбит }.

Тогда, так как , то . Следовательно, .