Линейная регрессия
РЕГРЕССИОННЫЙ АНАЛИЗ
Взаимосвязь между переменными величинами может быть описана разными способами. Например, как было показано в предыдущем разделе, эту связь можно описать с помощью различных коэффициентов корреляции (линейных, частных, корреляционного отношения и т.п.). В то же время эту связь можно выразить по-другому: как зависимость между аргументом (величиной) X и функцией Y. В этом случае задача будет состоять в нахождении зависимости вида Y = F(X) или, напротив, в нахождении зависимости вида Х= F(Y). При этом изменение функции в зависимости от изменений одного или нескольких аргументов называется регрессией.
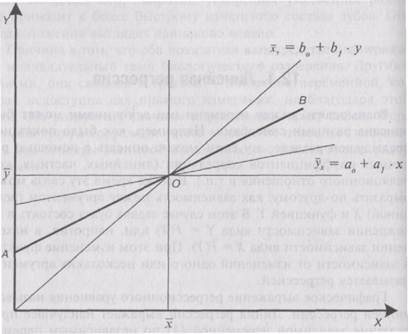
Графическое выражение регрессионного уравнения называют линией регрессии. Линия регрессии выражает наилучшее предсказание зависимой переменной (Y) по независимым переменным (X), Эти независимые переменные, а их может быть много, носят название предикторов.
Регрессию выражают с помощью двух уравнений регрессии, которые в самом простом случае выглядят, как уравнения прямой, а именно так:
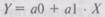(12.1)
(12.2)
В уравнении 12.1 Y — зависимая переменная, а X — независимая переменная, а0 свободный член, а а1 - коэффициент регрессии, или угловой коэффициент, определяющий наклон линии регрессии по отношению к осям координат.
В уравнении 12.2 X— зависимая переменная, а Y— независимая переменная, b0 свободный член, а b1 - коэффициент регрессии, или угловой коэффициент, определяющий наклон линии регрессии по отношению к осям координат.
