Начертательной геометрии
По
Конспект лекций
Калуга 2009
Лектор: Сломинская Е.Н.
Конспект лекций по начертательной геометрии
Калужский филиал
Выполнила: студентка группы ОПД – 12 Мосина Ю.В.
Метод проекций
Центральное проецирование
 S – центр проецирования
S – центр проецирования
А, В – точки в пространстве
α – плоскость проекций
S1, S2 – проецирующие лучи
А', В' – центральные проекции точек А и В на плоскость α
Параллельное проецирование
 Это частный случай центрального проецирования, когда центр проецирования отнесен в ∞. Проецирующие лучи превращаются в проецирующие прямые.
Это частный случай центрального проецирования, когда центр проецирования отнесен в ∞. Проецирующие лучи превращаются в проецирующие прямые.
S – направление проецирования
S1, S2 – проецирующие прямые
А', В' – параллельные проекции точек А и В на плоскость α
Ортогональное проецирование
Это частный случай параллельного проецирования, когда проецирующие прямые перпендикулярны плоскости проекции. При ортогональном проецировании φ=90˚.
Проецирование на две плоскости проекций
 А – точка в пространстве
А – точка в пространстве
π1 – горизонтальная плоскость проекции
π2 – вертикальная (фронтальная) плоскость проекции
А' – горизонтальная проекция точки А
А'' – фронтальная проекция точки А
Аx – проекция точки А на ось x
│А, π1│=zA
│А, π2│=yA
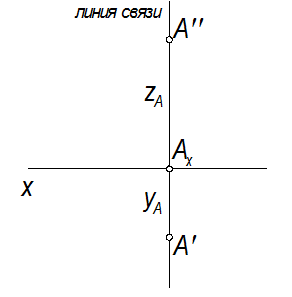
эпюр точки А
Проецирование на три плоскости проекций
 π3 – профильная плоскость проекции
π3 – профильная плоскость проекции
А''' – профильная проекция точки А
│А, π3│=хA
Чтобы построить профильную проекцию точки по двум данным, необходимо из фронтальной проекции провести горизонтальную прямую и отложить на ней от оси z «y» вправо, если он положителен, и влево от оси z, если отрицателен.
Прямая линия
Прямая линия – это множество точек – результат движения (перемещения) точки.
Линия может задаваться двумя проекциями.


Прямые общего и частного положения
Прямая общего положения – прямая не параллельная и не перпендикулярная ни одной из плоскостей проекций.
Прямые частного положения
1. Прямые уровня – это прямые, параллельные одной из плоскостей проекций.
горизонтальная прямая фронтальная прямая профильная прямая
уровня уровня уровня
a║ π1 b║ π2 c║ π3
а''║х, |а|=|а'| b'║х, |b|=|b''| c'Öх, c''Öх, |c|=|c'''|
β=(а^ π2)=(а'^ х) α=(b^ π1)=(b''^ х) α=(с^ π1), β=(с^ π2)



2. Проецирующие прямые – прямые, перпендикулярные одной из плоскостей проекций.
горизонтально фронтально профильно проецирующая прямая проецирующая прямая проецирующая прямая


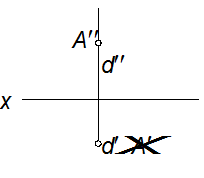 dÖ π1, d''Öх lÖ π2, l'Öх mÖ π3, m'║х, m''║х
dÖ π1, d''Öх lÖ π2, l'Öх mÖ π3, m'║х, m''║х
Определение действительной величины отрезка прямой общего положения и углов наклона его к плоскостям проекций
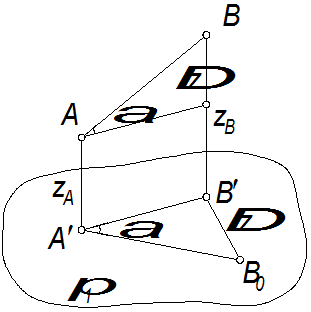

DZ=ZB-ZA, α – угол наклона ([AB]^π1), β – угол наклона ([AB]^π2)
Правило. Для определения действительной величины отрезка прямой общего положения необходимо построить прямоугольный треугольник, у которого один катет – горизонтальная (фронтальная) проекция отрезка, второй катет по величине равен разности расстояний концов отрезка, взятой с фронтальной (горизонтальной) проекции отрезков от оси х, гипотенуза этого треугольника равна действительной величине отрезка. Угол между гипотенузой (действительной величиной) и горизонтальной (фронтальной) проекцией отрезка равен углу наклона отрезка к горизонтальной (фронтальной) плоскости проекции.
Теорема 1. Если точка принадлежит прямой, то проекции точки принадлежат одноименным проекциям прямой.
Теорема 2. Если точка делит отрезок в каком-то соотношении, то одноименные проекции точки делят одноименные проекции отрезка в том же соотношении.
Следы прямой
Следы прямой – это точки пересечения прямой с плоскостями проекций.


На – горизонтальный след прямой
Fa – фронтальный след прямой
Взаимное расположение прямых
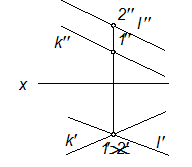


 1. а║b 2. c∩d 3. m║n 4. l – k
1. а║b 2. c∩d 3. m║n 4. l – k
1, 2 – конкурирующие точки, то есть точки, расположенные на одной проецирующей прямой.
Теорема о частном случае проецирования прямого угла
Если одна из сторон прямого угла параллельна плоскости проекций, а вторая – не перпендикулярна ей, то на эту плоскость проекций прямой угол проецируется в натуральную величину.
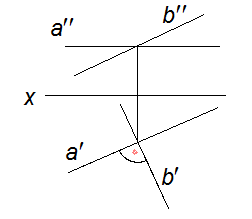
Плоскость
Способы задания плоскости
Плоскость в начертательной геометрии рассматривается как множество точек, линий; результат перемещения точек, линий.

 α (А, В, С) β (
α (А, В, С) β (
 А, b) γ (с║d) δ (m║n)
А, b) γ (с║d) δ (m║n)

α (DАВС)
Следы плоскости
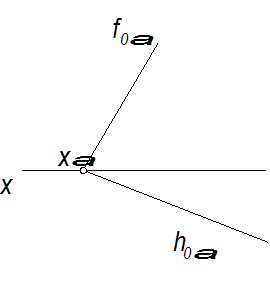
 Следы плоскости – это линии пересечения плоскости с плоскостями проекций.
Следы плоскости – это линии пересечения плоскости с плоскостями проекций.
α (h0α; f0α)
h0α – горизонтальный след плоскости
f0α – фронтальный след плоскости
Плоскость общего положения – это плоскость, не параллельная и не перпендикулярная ни одной из плоскостей проекций.
Плоскости частного положения
Плоскости уровня – это плоскости, параллельные какой-либо плоскости проекций.
Горизонтальная плоскость Фронтальная плоскость
уровня уровня
γ║π1 σ║π2

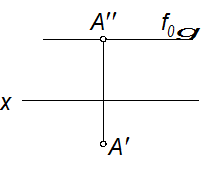
f0γ║x h0σ║x
Плоскости проецирования – это плоскости, перпендикулярные какой-либо плоскости проекций.
Горизонтально проецирующая Фронтально проецирующая
плоскость плоскость
αÖ π1 βÖ π1


f0α Ö х h0β Ö х
Теорема о принадлежности точки к плоскости
Если точка принадлежит прямой, принадлежащей плоскости, то она принадлежит этой плоскости.
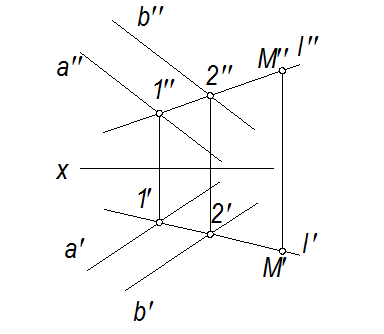
M l^l
l^l α(a║b)
α(a║b)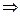 M
M α
α
Если прямая принадлежит плоскости, то следы прямой принадлежат одноименным следам плоскости.


Особые линии плоскости

 Горизонталь плоскости – это прямая, лежащая в плоскости и параллельная горизонтальной плоскости проекций.
Горизонталь плоскости – это прямая, лежащая в плоскости и параллельная горизонтальной плоскости проекций.
Все горизонтали одной и той же плоскости параллельны друг другу и параллельны горизонтальному следу плоскости.
Фронталь плоскости – это прямая, лежащая в плоскости и параллельная фронтальной плоскости проекций.
Фронтали одной и той же плоскости параллельны друг другу и параллельны фронтальному следу плоскости.
Линия наибольшего наклона – это линия, принадлежащая плоскости и перпендикулярная горизонтали плоскости (линия наибольшего ската) или фронтали плоскости (линия наибольшего наклона).
Взаимное положение прямых и плоскостей
1) Параллельность прямой и плоскости
Признак. Прямая параллельна плоскости, если она параллельна какой-либо прямой, расположенной в плоскости.
 m║l^l
m║l^l α(a∩b)
α(a∩b) m║α
m║α
2) Параллельность двух плоскостей
Признак. Если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны между собой.

α(а∩b) ^ β(c∩d) ^ a║c ^ b║d α║β
α║β
3) Перпендикулярность прямой и плоскости
Признак. Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в плоскости.


Если прямая перпендикулярна плоскости, то на эпюре ее фронтальная проекция перпендикулярна фронтальной проекции фронтали плоскости, а ее горизонтальная проекция перпендикулярна горизонтальной проекции горизонтали плоскости.
4)Перпендикулярность двух плоскостей
Признак. Если в одной из двух плоскостей есть прямая, перпендикулярная другой плоскости, то эти две плоскости перпендикулярны друг другу.


5) Пересечение прямой и плоскости
γÖπ 2
2
а – прямая общего положения

1) Заключить прямую в проецирующую плоскость
γ É а Ù γÖπ2
2) Строим линию пересечения
γ ∩ α(DАВС) = (1,2)
3) (1,2) ∩ а = К
α ∩ а = К
6) Пересечение плоскостей
α ∩ β
Для определения α ∩ β = l – линии пересечения плоскостей общего положения необходимо привлечь семейство посредников, это могут быть плоскости уровня или проецирующие.
 1. Применяем посредники – плоскость уровня γ1║π1 (горизонтальная плоскость уровня).
1. Применяем посредники – плоскость уровня γ1║π1 (горизонтальная плоскость уровня).
1.1 Найдем точки и линии пересечения посредника с плоскостями α и β
γ1 ∩ α = (1,2) = m1
γ1 ∩ β = (3,4) = p1
1.2 m1 ∩ p1 = К1 – первая общая точка для плоскостей
2. Вводим второй посредник
γ2║π1
2.1 γ2 ∩ α = (5,6) = m2
γ2 ∩ β = (7,8) = p2 2.2 m2 ∩ p2 = К2 3. (К1; К2) – α∩β) = l
Способы преобразования чертежа
На эпюре решение задач упрощается, если элементы задач имеют частное положение.
Для упрощения решений применяют способы преобразования чертежа, чтобы элементы задач перевести из общего положения в частное.
1)Способ замены плоскостей проекций.
Объект проецирования остается на месте, а плоскости проекций меняют свое положение по отношению к объекту проецирования.

Двойная замена плоскостей проекций.
Перевод отрезка общего положения в прямую уровня, а затем в проецирующую прямую.
 1. Ох
1. Ох  ® О1х1
® О1х1 
АВ оп ® АВ║π2,1
2.  О1х1® О2 х2
О1х1® О2 х2 
АВ оп® АВ║π2 ® АВÖπ1
αÖπ1 (π2) ®α║π1 (π2)
α (f0α; h0α)
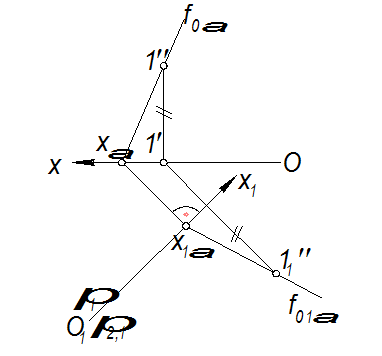
α (h0α; f0α) – о. п. ®
1.Ох  α(f0α; h0α) оп ® О1х1
α(f0α; h0α) оп ® О1х1  α (f0α; h0α) Öπ2,1
α (f0α; h0α) Öπ2,1
2) Вращение объекта вокруг оси, параллельной плоскости проекций (f или h).

1. j – о.п.®j н.в.
Произведем вращение вокруг горизонтали до совмещения угла j с плоскостью уровня, когда он спроецируется в натуральную величину.
1.1 h║π1 – произвольная
1.2 Объект вращения – А
1.3 Плоскость вращения (γÖh) (γÖπ1) (AÎγ)
1.4 γ∩h = O – центр вращения
1.5 ОА – радиус вращения
Вращение вокруг оси, перпендикулярной плоскости проекций

i – ось вращения
iÖπ1 (π2)
АВ – оп.® АВ║π1 (π2)
Поверхности
Поверхность – это траектория движущейся в пространстве линии.

Каркасный способ задания плоскости.
Определитель поверхности – это минимально необходимая и достаточная совокупность геометрических образов и связей между ними, однозначно определяющая поверхность.
Структурная формула определителя поверхности:
Ф(Г)[А]
Ф(g, d1, d2, d3)[gj∩d1, d2, d3≠Ø]
Классификация поверхностей

Поверхности вращения
Образованы вращением какой-либо линии вокруг оси.
 Кривая – плоская – все точки принадлежат одной плоскости.
Кривая – плоская – все точки принадлежат одной плоскости.
Горло – параллель с минимальным радиусом.
Экватор – параллель с наибольшим радиусом.
Секущая плоскость, проходящая через ось вращения, называется меридианальной плоскостью.
Если плоскость проходит через ось вращения, то это меридианальная плоскость.
Если меридианальная плоскость параллельна одной из плоскостей проекций, то такой меридиан – главный меридиан (фронтальный или горизонтальный).
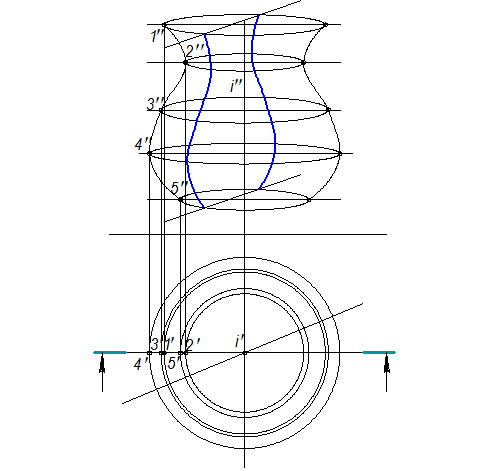
 Построение очерка поверхности, образованной вращением прямой, скрещивающейся с осью
Построение очерка поверхности, образованной вращением прямой, скрещивающейся с осью
Однополостный гиперболоид
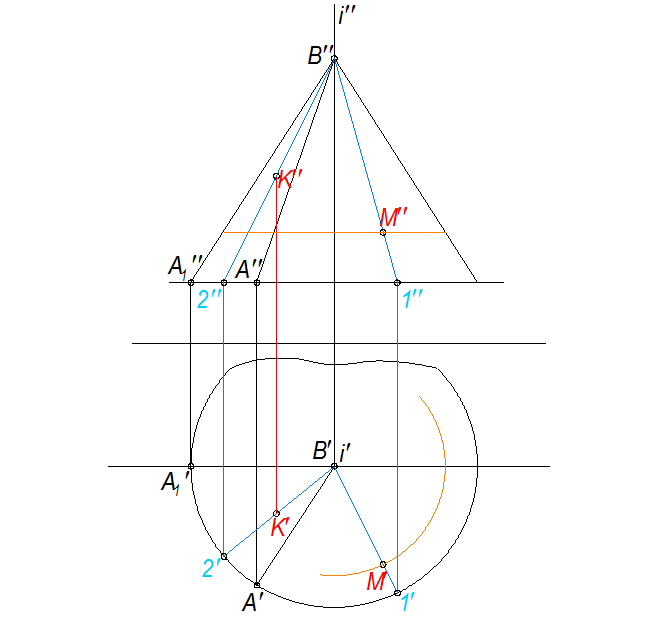 Построение очерка поверхности, образованной вращением прямой, пересекающейся с осью проекций
Построение очерка поверхности, образованной вращением прямой, пересекающейся с осью проекций
Поверхности, образованные вращением дуги окружности вокруг оси
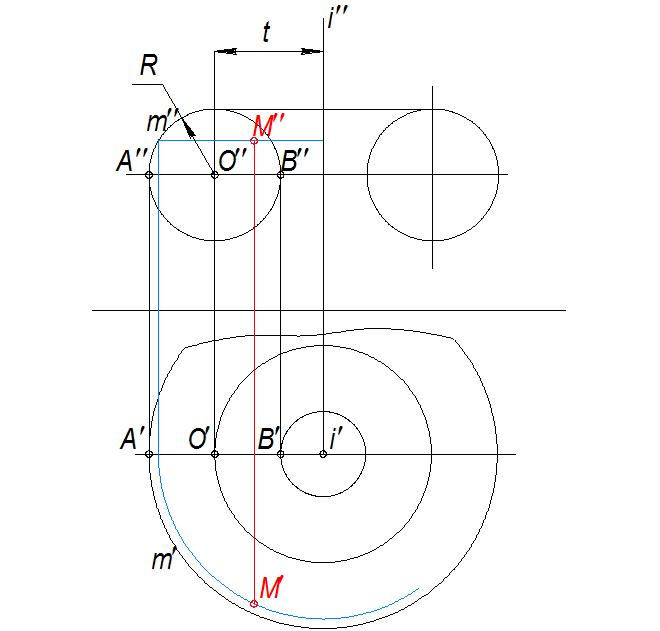 t>R – открытый тор, t≤R – закрытый тор, t=0 – сфера
t>R – открытый тор, t≤R – закрытый тор, t=0 – сфера

Сфера

Взаимное положение фигур
Линией пересечения фигур называется множество точек, принадлежащих одновременно этим двум фигурам.
Если одна из фигур занимает проецирующее положение, то построение линии пересечения значительно упрощается.



Алгоритм построения линии пересечения двух поверхностей
1. Для определения линии пересечения двух поверхностей находят ряд точек, общих для этих поверхностей, и соединяют их плавной кривой линией.
2. Для нахождения одной из точек, принадлежащих линии пересечения поверхностей:
1) Ввести вспомогательную поверхность.
2) Найти линии пересечения этой вспомогательной поверхности и двух заданных поверхностей.
3) Найти точку пересечения этих двух линий пересечения – это и есть одна из точек, принадлежащих линии пересечения, остальные точки находятся аналогично.
Замечание: в качестве вспомогательной необходимо выбирать такую поверхность, которая при пересечении с данными поверхностями дает простые линии – прямые или окружности. В качестве таких поверхностей часто выбирают плоскости, сферы, цилиндры и конусы.
Линия пересечения плоскости и поверхности
Плоская фигура, ограниченная линией пересечения плоскости и поверхности называется сечением.

Пересечение плоскости и поверхности вращения
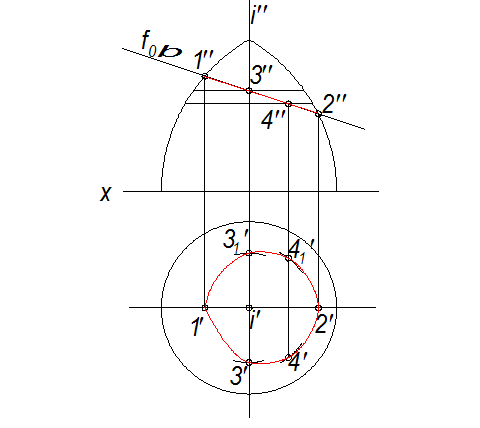
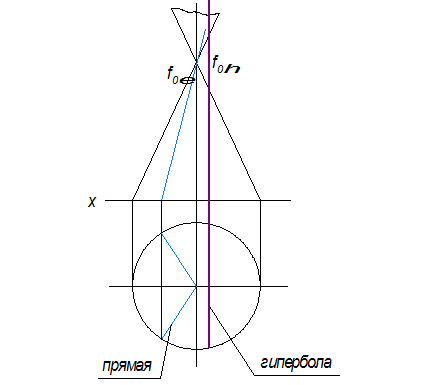
Конические сечения


Пересечение поверхностей
Метод секущих плоскостей.

Метод сфер.
Метод концентрических сфер.
Условия применения метода концентрических сфер:
1. Обе поверхности – поверхности вращения.
2. Оси поверхностей вращения пересекаются.
3. Обе поверхности имеют общую плоскость симметрии, образованную пересекающимися осями вращения, параллельную одной из плоскостей проекций.


Соосные тела вращения пересекаются по окружности, плоскость которой перпендикулярна их общей оси вращения.
Метод эксцентрических сфер.
Условия применения метода эксцентрических сфер:
1. Одна из поверхностей – поверхность вращения.
2. Вторая поверхность имеет кольцевые сечения.
3. Обе поверхности имеют общую плоскость симметрии, параллельную одной из плоскостей проекций.

Некоторые особые случаи пересечения поверхностей.
Теорема Монжа.
Если две поверхности второго порядка описаны вокруг третьей поверхности второго порядка или вписаны в нее, то линия пересечения распадается на две плоские кривые, плоскости которых пересекаются по линии, проходящей через точки пересечения линий касания.

Пересечение линии и поверхности.

Алгоритм
1. 1. Задается вспомогательная поверхность, заключающая линию.
2. 2. Строится линия пересечения вспомогательной поверхности и заданной.
3. 3. Находится точка пересечения линии пересечения и заданной линии.
Пересечение прямой линии с тором.

Пересечение линии и прямого кругового конуса.

Касание фигур.
Плоскостью, касательной к поверхности в данной точке, называется плоскость, являющаяся множеством прямых линий, каждая из которых является касательной к кривой линии, проведенной на поверхности через данную точку.
 Нормалью к поверхности называется прямая, перпендикулярная к касательной плоскости и проведенная через точку касания.
Нормалью к поверхности называется прямая, перпендикулярная к касательной плоскости и проведенная через точку касания.
Касание может происходить в точке или по линии.


Плоскость, касательная к поверхности вращения.
 Плоскость, касательная к поверхности тора в точке С, задается двумя пересекающимися прямыми, одна из которых является касательной к параллели, проведенной через точку С на поверхности тора (t1), вторая прямая является касательной к меридиану, проведенному через точку С на поверхности тора, и является образующей конуса, касательного к поверхности тора по параллели, проходящей через точку касания.
Плоскость, касательная к поверхности тора в точке С, задается двумя пересекающимися прямыми, одна из которых является касательной к параллели, проведенной через точку С на поверхности тора (t1), вторая прямая является касательной к меридиану, проведенному через точку С на поверхности тора, и является образующей конуса, касательного к поверхности тора по параллели, проходящей через точку касания.
Определение метрических характеристик геометрических фигур.
Определение расстояний.
К этим задачам относятся:
1. Определение расстояния между двумя точками.
2. Определение расстояния от точки до прямой.
3. Определение расстояния от точки до плоскости.
4. Определение расстояния между двумя скрещивающимися прямыми.
5. Определение расстояния между двумя параллельными прямыми.
6. Определение расстояния между двумя плоскостями.
1. Определение расстояния между двумя точками.
Методы решения:
1) прямоугольный треугольник;
2) вращение вокруг проецирующей прямой;
3) вращение вокруг прямой уровня;
4) замена плоскостей проекций.
2. Определение расстояния от точки до прямой общего положения.

1) α É A Ù α Ö a Ù α (h∩f)
2) α ∩ a = K
a) γ É а Ù γÖπ1
б) γ ∩ α = (1,2)
в) (1,2) ∩ а = К
3) 1A, a1 = 1[AK]1
3. Определение расстояния от точки до плоскости.

|
