Пример 2.

Пример 1.

1. - 1-го порядка;

2. - 3-го порядка.

Определение 4. Решениемдифференциального уравнения называется любая функция , которая при подстановке в это уравнение обращает его в тождество.

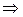
1. Функция является решением уравнения : , , - верно.

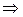
2. Функция является решением уравнения : - верно.

Определение 5.Процесс отыскания решения дифференциального уравнения называется его интегрированием, а график решения дифференциального уравнения – интегральной кривой.

Определение 6. Общим решениемдифференциального уравнения порядка называется такое его решение , которое является функцией переменно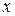й и произвольных постоянных .

Определение 7. Частным решением дифференциального уравнения порядка называется решение, получаемое из общего решения при подстановке вместо постоянных конкретных числовых значений.

Пример 3. Для дифференциального равнения общим решением является , а является одним из частных решений.

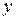Для того, чтобы составить дифференциальное уравнение, которому удовлетворяют кривые заданного семейства , следует продифференцировать это равенство раз, считая что - функция независимой переменной 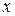, а затем из полученных равенств и исключить .

Пример 4. Составить дифференциальное уравнение семейства кривых .

Решение:

1) Дифференцируем заданную функцию 2 раза :

;

.

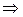
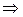
2) Исключим из этих двух уравнений постоянную :

.

Определение 8. Общим интегралом называется общее решение, записанное в неявном виде.

Определение 9. Частным интеграломназывается частное решение, записанное в неявном виде.

Решить дифференциальное уравнение - значит найти его общее решение или общий интеграл.