Решение

Результаты расчетов по методу Ирвина приведены в табл. 3.4.3.

Аномальными являются наблюдения 2, 3 и 16. На рис. 3.4.1. приведен график динамики временного ряда индекс потребительских цен, на котором второму и шестнадцатому наблюдениям соответствуют резкие выбросы.

Рис.3.4.1. График динамики временного ряда индекс потребительских цен.

Табл. 3.4.2. Индекс потребительских цен[2](% к предыдущему периоду)

Дата 4кв.1994 1кв.1995 2кв.1995 3кв.1995 4кв.1995 1кв.1996 2кв.1996 3кв.1996 4кв.1996 1кв.1997 2кв.1997 3кв.1997
№
Y(t) 142.77 124.92 115.21 113.02 110.01 105.08 100.8 104.57 105.29 103.03 100.5
                         
Дата 4кв.1997 1кв.1998 2кв.1998 3кв.1998 4кв.1998 1кв.1999 2кв.1999 3кв.1999 4кв.1999 1кв.2000 2кв.2000 3кв.2000
№
Y(t) 101.81 103.03 143.81 123.27 107.3 105.6 103.9 103.94 105.4 104.2
                         
Дата 4кв.2000 1кв.2001 2кв.2001 3кв.2001 4кв.2001 1кв.2002 2кв.2002 3кв.2002 4кв.2002 1кв.2003    
№    
Y(t) 105.4 107.1 105.3 101.1 104.1 105.5 103.4 101.2 104.26 105.2    

Табл. 3.4.3.Расчеты параметра .

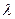t …
Y(t) 142.8 124.92 115.2 105.1 104.6 105.3 100.5 101.8 143.81 …
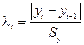
  4.028 1.681 0.915 0.206 0.28 0.464 0.4 0.355 0.068 0.21 0.238 0.123 0.115 0.191 4.032 … 0.09

 

Следующая процедура этапа предварительного анализа данных – выявление наличия тенденций в развитии исследуемого показателя. Отметим, что тенденция прослеживается не только в увеличении или уменьшении среднего текущего значения временного ряда, но она присуща и другим его характеристикам: дисперсии, автокорреляции, корреляции с другими показателями и т.д. тенденцию среднего визуально можно определить из графика исходных данных. Процедура проверки наличия или отсутствия неслучайной (и зависящей от времени t) составляющей по существу, состоит в статистической проверке гипотезы о неизменности среднего значения временного ряда:

Эта процедура может быть осуществлена с помощью различных критериев [Айвазян С.А., Мхитарян В.С.Прикладная статистика и основы эконометрики. М.: ЮНИТИ, 1998] приведем некоторые из них.

• Критерий серий, основанный на медиане. Расположим члены анализируемого временного ряда в порядке возрастания, т.е. образуем ряд:

.

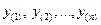Определим выборочную медиану по формуле

 

(3.4.4)

После этого мы образуем «серии» из плюсов и минусов, на статистическом анализе которых основана процедура проверки гипотезы о неизменности среднего значения временного ряда.

По исходному временному ряду, построим последовательность из плюсов и минусов следующим образом: вместо xt ставится «+», если 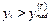, и «-», если (члены временного ряда, равные , в полученной таким образом последовательности плюсов и минусов не учитываются).

Образованная последовательность плюсов и минусов характеризуется общим числом серий n(n) и протяженностью самой длинной серии t(n). При этом под «серией» понимается последовательность подряд идущих плюсов и подряд идущих минусов. Если исследуемый ряд состоит из статистически независимых наблюдений, случайно варьирующих около некоторого постоянного уровня (т.е. справедлива гипотеза о неизменности среднего значения временного ряда), то чередование «+» и «-» в построенной последовательности должно быть случайным, т.е. эта последовательность не должна содержать слишком длинных серий подряд идущих «+» или «-», и, соответственно, общее число серий не должно быть слишком малым. Так что в данном критерии целесообразно рассматривать одновременно пару критических статистик (n(n); t(n)).

Справедлив следующий приближенный статистический критерия проверки гипотезы о неизменности среднего значения временного ряда:

если хотя бы одно из неравенств (3.4.5)

 

окажется нарушенным, то гипотеза о неизменности среднего значения временного ряда отвергается с вероятностью ошибки a, такой, что 0,05 < a < 0,0975 и, тем самым, подтверждается наличие зависящей от времени неслучайной составляющей в разложении Y(t) =f(t)+ S(t)+U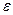(t)+(t).

• Критерий «восходящих» и «нисходящих» серий. Этот критерий «улавливает» постепенное смещение среднего значения в исследуемом распределении не тоько монотонного, но и более общего, например, периодического характера.

Так же, как и в предыдущем критерии, исследуется последовательность знаков - плюсов и минусов, однако правило образования этой последовательности в данном критерии иное. Здесь на i-ом месте вспомогательной последовательности ставится «+», если yi+1 - yi > 0, и «-», если yi+1 - yi < 0 (если два или несколько следующих друг за другом наблюдений равны между собой, то принимается во внимание только одно из них). Последовательность подряд идущих «+» (восходящая серия) будет соответствовать возрастанию результатов наблюдения, а последовательность «-» (нисходящая серия) - их убыванию. Критерий основан на том же соображении, что и предыдущий: если выборка случайна, то в образованной последовательности знаков общее число серий не может быть слишком малым, а их протяженность - слишком большой.

При уровне значимости 0,05 < a < 0,0975 критерий вид:

 

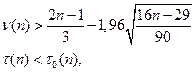(3.4.6)

где величина t0(n) определяется следующим образом:

n n£ 26 26 < n£ 153 153 < n£ 1170
t0(n) t0 = 5 t0 = 6 t0 = 7

Если хотя бы одно из неравенств (3.4.6) окажется нарушенным, то гипотезу о неизменности среднего значения временного ряда следует отвергнуть.

 

• Один из способов проверки обнаружения тренда основан на сравнении средних уровней ряда: временной ряд разбивают на две примерно равные по числу уровней части, каждая из которых рассматривается как некоторая самостоятельная выборочная совокупность, имеющая нормальное распределение. Если временной ряд имеет тенденцию к тренду, то средние, вычисленные для каждой совокупности, должны существенно (значимо) различаться между собой. Если же расхождение незначительно, несущественно (случайно), то временной ряд не имеет тенденции. Таким образом, проверка наличия тренда в исследуемом ряду сводится к проверке гипотезы о равенстве средних двух нормально распределенных совокупностей. Рассмотрим применение этого метода на следующем примере.