Смешанное (векторно-скалярное) произведение трех векторов.
Смешанным произведением трех векторов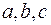 
называется произведение вида 
, где два первых вектора перемножаются векторно, а их произведение умножаются скалярно на третий вектор.
Смешанное произведение – величина скалярная, так как последнее действие – скалярное умножение.
Абсолютная величина смешанного произведения некомпланарных векторов 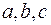равна объему параллелепипеда, построенного на этих векторах, причем знак его зависит от ориентации этих векторов: если 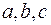образуют правую тройку, то их смешанное произведение будет положительно, для левой же тройки – отрицательно.
Свойства смешанного произведения
1. Смешанное произведение не изменяется:
1) если перемножаемые вектора переставлять в круговом порядке: 
2) если поменять местами знаки векторного и скалярного умножения: 
, поэтому можно записать 
.
2. Перестановка в смешанном произведении любых двух векторов изменяет лишь его знак: 
; 
; 
.
3. Смешанное произведение обращается в нуль, если
1) хотя бы один из перемножаемых векторов есть нуль-вектор;
2) два из перемножаемых векторов коллинеарны;
3) три перемножаемых вектора компланарны.
Вычисление смешанного произведения
трех векторов, разложенных по ортам
; 
; 
, то
Вычисление объема четырехгранной пирамиды (тетраэдр)
Объем такой пирамиды равен одной шестой объема параллелепипеда, построенного на его сходящихся в одной вершине ребрах. А объем этого параллелепипеда – абсолютная величина смешанного произведения трех векторов, общее начало которых находится в одной из вершин пирамиды, а концы – в остальных трех ее вершинах. Если вершинами пирамиды служат точки 
, 
, 
, 
, то полагая 
; 
; 
, получим 
.
Условие компланарности трех векторов
Три вектора 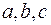компланарны тогда и только тогда, когда их смешанное произведение равно нулю: 
или 
.