Векторное произведение двух векторов.
Векторным произведением вектора 
на вектор 
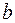называется новый вектор 
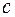, обозначаемый символом 
, и определяемый следующими тремя условиями:
1) модуль вектора 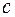равен площади параллелограмма, построенного на векторах и 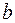(после совмещение их начал), то есть 
, где 
– угол между векторами и .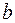
2) Вектор 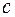перпендикулярен к плоскости этого параллелограмма (то есть перпендикулярен обоим векторам и ).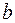
3) Вектор 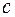направлен в ту сторону от этой плоскости, что кратчайший поворот от вектора к вектору 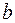вокруг вектора 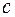(после совмещения начал всех трех векторов) кажется происходящим против часовой стрелки, если смотреть из конца вектора 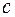(то есть вектора , 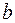и 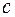должны образовывать правую тройку).
| Выражение скалярного произведения <== предыдущая | | | следующая ==> Свойства векторного произведения |
Дата добавления: 2014-01-25; просмотров: 203; Опубликованный материал нарушает авторские права?.