Системы координат.

Фиксируем в пространстве т.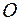и рассматриваем произвольную точку . Радиусом-вектором т.по отношению к точке 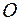называется вектор . Если в пространстве кроме точки 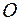выбран некоторый базис, то точке можно сопоставить упорядоченную тройку чисел – компоненты ее радиус-вектора.

Декартовой системой координат в пространстве называется совокупность точки и базиса.

Точка носит название начала координат; прямые, проходящие через начало координат в направлении базисных векторов, называются осями координат. Первая – ось абсцисс, вторая – ось ординат, третья – ось аппликат. Плоскости, проходящие через оси координат, называются координатными плоскостями.

Рассмотрим прямоугольную систему координат в пространстве . На каждой из осей выберем единичный вектор, направление которого совпадает с положительным направлением оси: векторы , причем . Эти три взаимно-перпендикулярных вектора называются ортами. Так как эти орты некомпланарны, то они образуют базис, называемый декартовым ортогональным. Рассмотрим некоторый вектор в пространстве, переместим его в точку 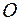, то есть построим . Проведя через конец вектора плоскости, параллельные координатным осям, получим параллелепипед.

, где ; .

Векторы – составляющие вектора по осям , , .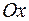

, , .

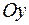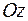Обозначим проекции вектора на оси , , – .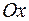

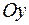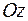Тогда, разложение вектора по ортогональному базису будет таким: .

Это разложение вектора на составляющие по координатным осям. Если проекции вектора на оси координат равны , то можно записать: . Это прямоугольные декартовы координаты.

Линейные операции над векторами можно заменить арифметическими действиями над их проекциями:

,

.

Направление вектора в пространстве определяется углами , которые вектор составляет с осями координат.

Косинусы этих углов называются направляющими косинусами вектора :

, то есть ;

, то есть ;

, то есть .

Вектор – диагональ параллелепипеда, а зная теорему о диагонали прямоугольного параллелепипеда: и ; получим .

Условия коллинеарности двух векторов

Для коллинеарности двух векторов необходимо и достаточно, чтобы их проекции были пропорциональны: .

Деление отрезка в данном отношении.

Отношение, в котором точка М делит отрезок М₁М₂ , называется число , удовлетворяющее равенству . Связь между координатами делящей точки М(x,y,z), точек M₁(x₁,y₁,z₁), M₂(x₂,y₂,z₂) и числом задается равенствами:

Деление отрезка M₁M₂ , будет внутренним, если >0, и внешним <0. При =1 точка М будет серединой отрезка M₁M₂. ≠ -1.