Векторная алгебра. Основные понятия и определения.

Тема Векторы и координаты.

ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ.

Изучение связи между качественными признаками на основе таблиц сопряженности

 

Качественные (неколичественные) признаки (пол, образование, семейное положение, профессия, форма собственности и т.п.), взаимосвязи между ними, их влияние на другие показатели (в том числе и количественные) часто приходится изучать при проведении различных социологических исследований путем опроса или анкетирования.

 

 

 

[1] В вариационных рядах варианты могут быть представлены конкретными числами или интервалами, в первом случае вариационный ряд является дискретным, а во втором - интервальным.

[2] Если статистический ряд интервального типа, то в качестве вариант используют середины интервалов.

[3] Формула средней геометрической получается из средней степенной после раскрытия неопределенности при вычислении предела .

[4] Закон распределения Пуассона также называют законом редких явлений, так как он справедлив при вероятности наступления исследуемого события p≤0,1 и больших (порядка сотен единиц) объемах выборок n.

[5] Для точности расчетов будем использовать исправленное выборочное среднее квадратическое отклонение , получаемое на основе исправленной выборочной дисперсии . Более подробно об исправленной выборочной дисперсии см. §

[6] ; - нормированное отклонение.

[7] Использование в формулах знака ≈ вместо = объясняется тем, что в практике исследований зачастую отсутствует информация о вариации признака в генеральной совокупности (в частности, о дисперсии), поэтому нередко при расчетах пользуются их приближенными значениями (оценками), вычисленными по выборке.

[8] При серийной выборке повторный отбор практически не применим, поэтому в основном используются формулы средней квадратической ошибки для бесповторного способа отбора.

[9] В практике чаще встречаются равновеликие серии, в случае неравновеликих серий необходимо использовать аналогичную взвешенную формулу (т.е. учитывать веса серий – количество единиц серий).

[10] За исключением случая, если изначально известно, что изучаемый признак Х генеральной совокупности имеет нормальное распределение N(,σ²), то выборочная средняя при любом n (а не только при ) имеет нормальный закон распределения N(,).

[11] Значения функции распределения Стьюдента приведены в приложении 2.

Вектор – отрезок определенной длины, одна из ограничивающих точек которого принята за начало, а другая – за конец.

Длина вектора (модуль) – расстояние между ограничивающими его точками.

Вектор называется нулевым, если его начало и конец совпадают.

Векторы называются коллинеарными, если они располагаются на одной прямой или на параллельных прямых, то есть если существует прямая, которой они параллельны.

Векторы называются сонаправленными если направление этих векторов совпадает. Нулевой вектор считается сонаправленным с любым другим вектором.

Векторы называются противоположно-направленными если лежат на параллельных прямых и имеют противоположное направление.

Векторы называются компланарными, если они лежат в одной плоскости или если существует плоскость, которой они параллельны. Если компланарные векторы имеют общее начало, то они лежат в одной плоскости.

Векторы называются равными, если они имеют равные модули, коллинеарны и направлены в одну сторону.

Вектор можно переносить параллельно самому себе, помещая его начало в любую точку пространства.

Сложение векторов

Пусть даны два вектора и .

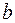1. Возьмем произвольную точку 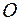и построим вектор 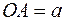, потом от этой же точки отложим вектор 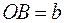. Построим на этих векторах, как на сторонах, параллелограмм 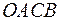. Вектор 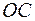, являющийся диагональю параллелограмма, проведенной из вершины 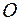, и будет суммой векторов .

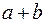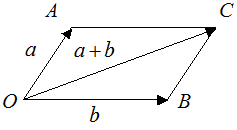
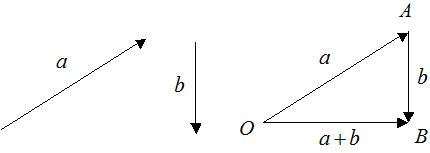
2. От произвольной точки 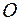отложим вектор 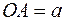, затем от точки 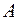отложим вектор 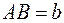. Вектор, соединяющий начало первого слагаемого с концом второго, будет суммой этих векторов .

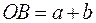Свойства сложения векторов

I. Сложение векторов коммутативно (переместительное свойство): .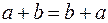

II. Сложение векторов ассоциативно (сочетательное свойство): .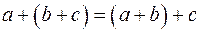

Сумму любого конечного числа векторов можно построить по следующему правилу: из произвольной точки 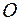откладывается вектор, равный первому слагаемому вектору. К концу первого вектора присоединяется начало второго, к концу второго – начало третьего и т.д. Суммой данных векторов будет вектор, соединяющий начало первого вектора с концом последнего.

Разность векторов– это третий вектор 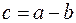, сумма которого с вычитаемым вектором 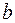дает .

Правило построения вектора разности: откладываем векторы 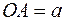и 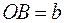из общей точки 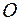. Вектор, соединяющий концы уменьшаемого вектора и вычитаемого вектора 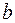, и направленный от вычитаемого к уменьшаемому, и будет разностью векторов и.

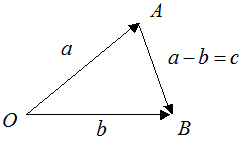
Если на векторах и , отложенных из общей точки, построить параллелограмм, то вектор 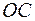(одна диагональ параллелограмма) равен сумме 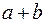, а вектор 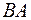(другая диагональ) равен разности .

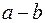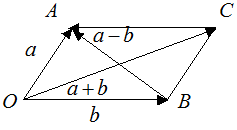
Умножение вектора на скаляр

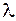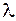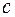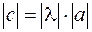Пусть даны вектор и число . Произведением вектора на число называется вектор , коллинеарный вектору , имеющий длину и то же направление, что и вектор , если 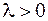, и противоположное направление, если .

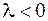Из определения умножения вектора на число следует, что если 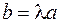, то векторы 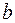и коллинеарны. Очевидно, что из коллинеарности векторов следует, что .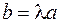

Теорема 1. Двавектора и 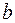коллинеарны тогда и только тогда, когда имеет место равенство .

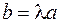1). Для любых чисел 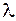и 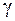и любого вектора справедливо равенство .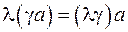

2). Пусть существует вектор , не равный нулю. Для любого коллинеарного ему вектора 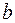существует, и притом только одно 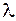, удовлетворяющее равенству: .

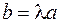Это число либо 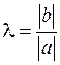, либо 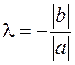в зависимости от того направлены ли вектора и 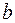одинаково или противоположно.

Умножение вектора на число обладает распределительным свойством , .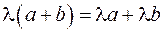

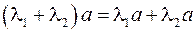Вектор, длина которого равна единице, называется единичным.

Каждый вектор равен произведению его модуля на единичный вектор того же направления (это следует из определения умножения вектора на число).

Угол между двумя векторами

Пусть даны два произвольных вектора и 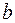. Отложим от произвольной точки векторы 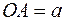, 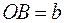. Угол между векторами – это угол, на который надо повернуть один из векторов до его совпадения со вторым.

Рассмотрим ось 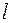, положительное направление которой совпадает с направлением единичного вектора 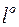, расположенного на оси. Тогда, углом между вектором и осью будет угол между векторами , .

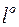Проекция вектора на ось и составляющая вектора по оси

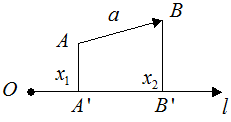
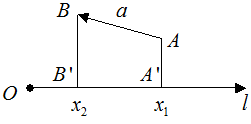
Проекцией вектора на ось 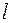называется длина отрезка 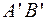, заключенного между основаниями перпендикуляров, опущенных на ось из начала и конца вектора , которой приписан знак «+», если отрезок 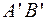ориентирован в положительную сторону относительно 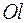и знак “–“, если наоборот.

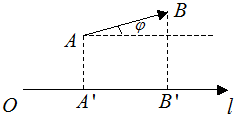
Теорема 1:Проекция вектора на ось 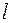равна модулю вектора , умноженному на косинус угла между вектором и осью: .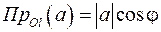

Теорема 2: Проекция суммы двух векторов на ось равна сумме проекций слагаемых векторов на ту же ось ; .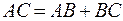

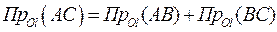Теорема 3: если вектор a умножить на число 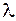, то его проекция на ось также умножится на это число: .

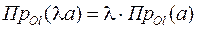Вектор, соединяющий проекцию начала вектора с проекцией его конца, называется составляющей вектора по оси : .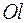

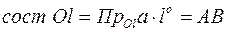Линейная зависимость векторов

Векторы 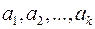называются линейно зависимыми, если существуют числа 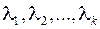, не все равные нулю, для которых имеет место равенство .

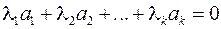Векторы 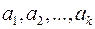называются линейно независимыми, если равенство (I) имеет место только при 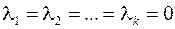(то есть в тривиальном случае).

Если несколько векторов линейно зависимы, то хотя бы один из них всегда можно представить в виде линейной комбинации остальных (верно и обратное).

Линейная зависимость векторов на плоскости

Теорема 1:всякие три вектора 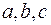на плоскости линейно зависимы.

Следствие:Если число данных векторов на плоскости больше трех, то они также линейно зависимы, то есть один из них можно представить в виде линейной комбинации остальных.

Теорема 2:Для того чтобы два вектора на плоскости были линейно независимы, необходимо и достаточно, чтобы они были неколлинеарны.

Два коллинеарных вектора линейно зависимы.

Максимальное число линейно независимых векторов на плоскости равно двум.

Линейная зависимость в пространстве

Теорема 3: всякие четыре вектора 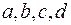в пространстве линейно зависимы.

Следствие:

1) Если число векторов в пространстве больше четырех, то они линейно зависимы.

2) Для того, чтобы три вектора были компланарны, необходимо и достаточно, чтобы они были линейно зависимы.

3) Максимальное число линейно независимых векторов в пространстве равно трем.

Базисом на плоскости называются два любых линейно независимых вектора. Пусть 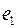и 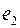образуют базис. Любой вектор на плоскости можно представить в виде: 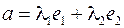(так как три вектора на плоскости линейно зависимы), то есть разложить по базису.

Числа 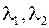– аффинные координаты вектора на плоскости .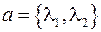

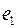Теорема 4: разложение вектора по базису и 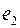является единственным.