Преобразование координат в векторном пространстве.

Всё сказанное в этом параграфе верно для векторного пространства Lⁿпроизвольной размерности. Но для облегчения восприятия этого материала мы ограничимся случаем n = 3.

Пусть в векторном пространстве L³выбраны два произвольных базиса B = {e₁, e₂, e₃} и B¢= {e₁¢, e₂¢, e₃¢}. Пусть один и тот же вектор x в первом и втором базисе имеет соответственно координаты x(x₁, x₂, x₃)_B иx(x ₁¢, x ₂¢, x₃¢)_B¢. Требуется найти связь между этими координатами.

Для решения этой задачи нам должно быть известно, как векторы второго базиса раскладываются по первому базису:

e₁¢ = c₁¹e₁ + c₁²e₂ + c₁³e₃,

e₂¢ = c₂¹e₁ + c₂²e₂ + c₂³e₃, (9)

e₃¢ = c₃¹e₁ + c₃²e₂ + c₃³e₃,

Из коэффициентов этого разложения мы составляем матрицу

C = , (10)

которая называется матрицей перехода от первого базиса ко второму. Пишем так: B B¢. При составлении этой матрицы мы коэффициенты из каждой строчки в записывали в соответствующий по номеру столбец. В соответствии с определением, что такое координаты, мы можем записать разложения вектора x по первому и второму базисам:

x = x₁e₁ + x₂e₂ + x₃e₃ (11.1)

x = x₁¢ e₁¢ + x₂¢ e₂¢ + x₃¢ e₃¢ . (11.2)

Подставим в последнее равенство разложения (9):

x = x₁¢ (c₁¹e₁ + c₁²e₂ + c₁³e₃) + x₂¢ (c₂¹e₁ + c₂²e₂ + c₂³e₃) + x₃¢ (c₃¹e₁ + c₃²e₂ + c₃³e₃).

Раскроем скобки и сгруппируем коэффициенты при одинаковых векторах:

x = (c₁¹x₁¢ + c₂¹x₂¢ + c₃¹x₃¢ )e₁ + (c₁²+ c₂²x₂¢ + c₃²x₃¢ )e₂ + (c₁³+ c₂³x₂¢ + c₃³x₃¢ )e₃.

Сравним это выражение с (11.1). В силу единственности разложения вектора по базису, получаем

x₁= c₁¹+ c₂¹x₂¢ + c₃¹x₃¢ ,

x₂ = c₁²+ c₂²x₂¢ + c₃²x₃¢ , (12)

x₃ = c₁³+ c₂³x₂¢ + c₃³x₃¢ .

Если использовать столбцы, составленные из координат

X = , X¢ = .

То систему (12) можно переписать в виде одного матричного равенства:

X = CX¢. (12¢)

Эти формулы позволяют найти координаты вектора в первом базисе, если известны его координаты во втором, т.е. они выражают «обратную связь». Для того, чтобы найти прямую связь мы из (12¢) выражаем

X ¢= C^–1X, (13¢)

Таким образом, вторые координаты выражаются через первые по формулам

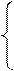= b₁²x₁ + b₂²x₂ + b₃²x₃,

x₂¢ = b₁²x₁ + b₂²x₂ + b₃²x₃, (13)

x₃¢ = b₁³x₁ + b₂³x₂ + b₃³x₃,

где B = C ^–1, т.е. коэффициенты b_i^jберутся из матрицы, обратной к матрице перехода. Вместо того чтобы искать обратную матрицу, можно решить систему уравнений (12) относительно неизвестных x₁¢ , x₂¢ , x₃¢ и мы получим те же формулы (13).

Предположим теперь, что оба базиса B = {e₁, e₂, e₃} и B¢= {e₁¢, e₂¢, e₃¢} являются ортонормированными. Тогда должно выполняться

e₁¢² = (c₁¹)² + (c₁²)² + (c₁³)² = 1,

e₁¢·e₂¢ = c₁¹·c₂¹ + c₁²·c₂² + c₁³·c₃² = 0.

И аналогично, сумма квадратов элементов каждого столбца матрицы C равна 1, а сумма произведений элементов одного столбца матрицы C на соответствующие элементы другого столбца равна нулю. Матрица, обладающая такими свойствами, является ортогональной, т.е. для неё выполнено C·C^T= E (это изучается в курсе алгебры). Другими словами, для ортогональной матрицы обратная матрица совпадает с транспонированной. Переход от одного ОНБ к другому осуществляется с помощью ортогональной матрицы.