ЛЕКЦИЯ 8: Абсолютные и относительные величины в статистике. Средние величины в статистике

Статистический показатель – количественная характеристика социально-экономические процесса или явления.

Совокупность взаимосвязанных статистических показателей, имеющая одноуровневую или многоуровневую структуру, образует систему статистических показателей.

Отличают показатели – категории и конкретные статистические показатели. Показатель – категория отражает сущность, общие отличительные свойства конкретных статистических показателей. Но после привязки к конкретному месту (объекту), он становится конкретным. Например, численность населения – качественное определение, а численность населения г. Лениногорск на 01.01.2010г. – конкретный статистический показатель.

По охвату единиц совокупности показатели могут быть индивидуальные и сводные. Сводные делятся на:

· объемные – получают путем сложения значений признака отдельных единиц совокупности

· расчетные - вычисляются по различным формулам и служат для измерения взаимосвязи, вариации, характеристики структурных сдвигов и т.д.

По временному фактору показатели могут быть моментными – на дату и интервальными – за период, от …до …

По пространственному признаку показатели могут относиться к федеральному, региональному и местному уровню.

С точки зрения конкретных объектов и формы выражения, показатели могут быть абсолютными, относительными, средними.

Статистические показатели, выражающие раз­меры (объемы, уровни) социально-экономических явлений в еди­ницах меры, веса, объема, протяженности, площади, стоимости и т.д. называются абсолютными статистическими величинами. Они всегда имеют определенную размерность, определенные единицы измерения.

Выбор единиц измерения абсолютных величин определяется сущностью, свойствами изучаемого явления, а также задачами исследования. В статистике применяется большое число самых разнообразных единиц измерения. В самой общей клас­сификации их можно свести к трем типам: натуральные, денежные (стоимостные) и трудовые.

Натуральными принято называть такие единицы измерения, ко­торые выражаются в мерах веса, объема, длины, площади и т.д. Такими единицами измерения пользуются для характеристики объе­ма различных видов продукции, размеров продажи товаров, мощ­ности электростанций и т.д. Таковы производство тканей - в по­гонных и (или) квадратных метрах, производство газа - в кубичес­ких метрах, электроэнергии - в киловатт-часах.

В ряде случаев применяются условно натуральные единицы из­мерения. Они используются для сведения воедино нескольких раз­новидностей одной и той же потребительской стоимости. Одну из них принимают за эталон, а другие пересчитываются с помощью специальных коэффициентов в единицы меры этого эталона. Так, в практике нашей статистики пересчитываются все виды топлива в условное топливо с теплотой сгорания 29,3 МДж/кг (7000 ккал/кг).

Мыло с различным содержанием жировых кислот пересчитывается на 40%-ное содержание жирных кислот, консервы разного объе­ма - в условные консервные банки объемом 353,4 см3, грузовые ва­гоны- в двухосные и т.д.

Если, допустим, имеется 100 т мыла с содержанием жировых кислот в 40% и 100 т с содержанием жиро­вых кислот в 60%, то, пересчитав на 40%-ное мыло, получим 100 + 100 • 60/40 = 250 условных тонн мыла.

Трудовые единицы измерения такие, как человеко-часы, человеко-дни и т.д., используются для определения затрат труда на про­изводство продукции, на выполнение какой-нибудь работы, на учет трудоемкости отдельных операций технологического про­цесса.

В условиях рыночной экономики большое значение и широкое применение имеют стоимостные единицы измерения, дающие де­нежную оценку социально-экономическим явлениям и процессам.

Таковы: валовой внутренний продукт, товарооборот, доходы и рас­ходы населения и др.

Абсолютные статистические показатели подразделяются на по­казатели объема и показатели уровня.

Показатели объема позволяют характеризовать величину всей совокупности или ее частей. Так, численность экономически актив­ного населения в России в 1998 г. составила 72 572 тыс. человек, в том числе мужчин 38355 тыс. человек, женщин - 34217 тыс. чело­век. Они могут также выражать суммарную величину какого-либо признака всей совокупности или ее части.

Показатели уровня характеризуют величину нагрузки единицы одной совокупности элементами другой совокупности (например, в России в 1999 г. число жителей на 1 км2 территории составило 8,6 чел.). Они могут определять и степень насыщенности конкретной совокупности элементами какого-то признака данной или другой совокупности. (в России в 1998 г. величина прожиточного минимума в среднем на душу населения в месяц составила 493,3 руб.; в 1998 г. в Москве средняя розничная цена на пальто женское демисезонное из шерстяных и полушерстяных тканей составила 2128,16 руб. за штуку).

Существуют также разностные абсолютные показатели. Они пред­ставляют собой абсолютный размер в различии двух абсолютных по­казателей во времени или в пространстве. Примером абсолютного по­каза геля разности во времени (называемого абсолютным показателем прироста) может служить разность между производством кондитерс­ких изделий и России в 1998 г. (1310 тыс. т) и в 1992 г. (1829 тыс. т), равная 519 тыс. т. Па эту величину за шесть лет уменьшился абсо­лютный размер производства кондитерских изделий в России

Относительными показателями называются статистические по­казатели, определяемые как отношение сравниваемой абсолютной величины к базе сравнения. Величина, с которой производится срав­нение (знаменатель дроби) обычно называется основанием, базой сравнения или базисной величиной. Числитель - сравниваемая ве­личина. Ее называют также текущей или отчетной величиной.

На­пример, разделив численность городского населения на всю чис­ленность населения страны, получаем показатель «доля городско­го населения».

Сопоставляемые величины могут быть одноимен­ными и разноименными. Если сравниваются одноименные величи­ны, то относительные показатели выражаются в отвлеченных чис­лах. Как правило, базу сравнения принимают равной 1,100,1000 или 10000. Если основание равно 1, то относительная величина пока­зывает, какую долю от базисной составляет текущая величина. Если база сравнения равна 100, то относительная величина выражена в процентах (%), если база сравнения равна 1000 - в промилле (%о), 10000 - в продецимилле (%оо).

При сопоставлении разноименных величин наименования относи­тельных величин образуются от наименований сравниваемых величин (плотность населения страны: чел./км2; урожайность: ц/га и т. д.).

В зависимости от задач, содержания и значения выражаемых коли­чественных соотношений различают относительные показатели пла­нового задания, выполнения плана, динамики, структуры, координа­ции, сравнения, интенсивности, уровня экономического развития.

Относительные показатели планового задания (ОППЗ) использу­ются в целях перспективного планирования деятельности субъек­тов финансово-хозяйственной сферы, а также для сравнения реаль­но достигнутых результатов с ранее намеченными.

Пример В I квартале розничный товарооборот торгового объединения составил 250 млн руб., во II квартале планируется роз­ничный товарооборот в 350 млн руб. Определить относительную величину планового задания.

Решение: ОППЗ * 100% = 140%. Таким образом, во II квар­тале планируется увеличение розничного товарооборота торгово­го объединения на 40%.

Относительные показатели выполнения плана (ОПВП) выража­ют соотношение между фактическим и плановым уровнями пока­зателя. Обычно они выражаются в процентах. Способ вычисления относительных показателей выполнения плана зависит от того, в каком виде и в какой форме даны показатели плана. Плановые по­казатели могут быть установлены в виде абсолютных и средних ве­личин. Если плановое задание установлено в виде абсолютных и средних величин, степень выполнения плана определяется путем деления фактически достигнутой величины показателя на величи­ну, предусмотренную планом

Когда план задан в виде относительного показателя (по сравне­нию с базисным уровнем), выполнение плана определяется из соот­ношения относительной величины динамики с относительной ве­личиной планового задания

Если плановое задание предусматривает снижение уровня пока­зателя, то результат сравнения фактического уровня с запланиро­ванным, составивший по своей величине менее 100%, будет свиде­тельствовать о перевыполнений плана.

Относительными показателями динамики (ОПД) называют ста­тистические величины, характеризующие степень изменения изуча­емого явления во времени. Они представляют собой отношение уровня исследуемого процесса или явления за данный период вре­мени и уровня этого же процесса или явления в прошлом.

Рассчитанная таким образом величина показывает, во сколько раз текущий уровень превышает предшествующий (базисный) или какую долю от последнего он составляет. Данный показатель мо­жет быть выражен в долях или в процентах.

При наличии данных за несколько периодов времени сравнение каждого данного уровня может производиться либо с уровнем пред­шествующего периода, либо с каким-то другим, принятым за базу сравнения (базисным уровнем). Первые называются относитель­ными показателями динамики с переменной базой сравнения, или цепными, вторые - относительными показателями динамики с по­стоянной базой сравнения, или базисными. Относительные пока­затели динамики иначе называются темпами роста и коэффициен­тами роста.

Между относительными показателями планового задания, вы­полнения плана и динамики существует следующая взаимосвязь: ОППЗ • ОПВП = ОПД. Основываясь на этой взаимосвязи, по лю­бым двум известным показателям всегда можно определить третью неизвестную величину.

Относительные показатели структуры (ОПС) представляют со­бой отношение части и целого. Они характеризуют структуру, со­став той или иной совокупности социально-экономических явле­ний. Из определения относительных показателей структуры следу­ет, что при их исчислении в качестве базы сравнения берется вели­чина целого (общий итог по какому-либо показателю), а сравнива­емыми являются значения показателей отдельных частей этого це­лого.

Относительные показатели координации (ОПК) представляют собой соотношение одной части совокупности к другой части этой же совокупности

В результате этого деления получают, во сколько раз данная часть совокупности больше (меньше) базисной, или сколько про­центов от нее составляет, или сколько единиц данной структурной части приходится на 1 единицу, на 100, на 1000 и т. д. единиц дру­гой части, принятой за базу сравнения.

Относительные показатели интенсивности (ОПИ) характеризу­ют степень насыщенности или развития данного явления и пред­ставляют собой отношение исследуемого показателя к размеру при­сущей ему среды

Разновидностью относительных показателей интенсивности яв­ляются относительные показатели уровня экономического развития (ОПУЭР). Они характеризуют выпуск продукции в расчете на душу населения и весьма значимы при оценке состояния экономики го­сударства.

Поскольку объемные показатели производства по своей приро­де являются интервальными, а показатель численности населения - моментным, в расчете используют среднюю за период численность населения (например, среднегодовую):

Относительные показатели сравнения (ОПСр) представляют со­бой отношение одноименных величин, относящихся к разным объектам (предприятиям, фирмам, районам, областям, странам и т.п.):

С помощью такого показателя можно сравнивать численность населения, размеры территории, величину посевных площадей по странам, областям, районам и т. д.

 

Средние величины являются самыми распространенными в статистике. Они представляют собой обобщенную количественную характеристику признака, в статистической совокупности. Они дают обобщенную характеристику однотипных явлений по одному из варьирующих признаков.

Важнейшим свойством средних величин является способность отражать общее присущее всем единицам совокупности. Средняя величина отражает типичный уровень признака, когда она рассчитывается по качественно однородной совокупности. Если совокупность не однородная общее среднее значение следует дополнить групповыми средними величинами, которые рассчитываются в результате предварительной группировки данных совокупности.

Наиболее распространенными видами средних, используемых в статистике относят:

- арифметическая, которая может быть простой и взвешенной.

Среднеарифметическая простая используется, когда расчет осуществляется по не сгруппированным данным. Для этого сумма значений варьирующих показателей делится на их суммарное количество.

 

Среднеарифметическая взвешенная, используется при повторяющемся значение вариативного признака. В этом случае определяется частота повторения такого значения и средняя рассчитывается по сгруппированным данным по формуле:

 

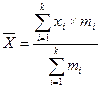
или по формуле:

 

Где Х –

т -

При расчете средней взвешенной по данным интервального ряда, необходимо перейти от интервальных значений к срединным значениям.

Среднегармоническая взвешенная - используется когда известен числитель исходного соотношения средней, но не известен ее знаменатель. В этом случае расчет осуществляется по формуле:

, где w_i = x_im_i

Средняя геометрическая невзвешенная - может использоваться место взвешенной в тех случаях, когда значения w_i для единиц совокупности равны (плановая продолжительность рабочего дня). Она рассчитывается по формуле:

 

 

 

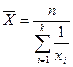
Средняя геометрическая невзвешенная рассчитывается по формуле:

 

 

Средняя гармоническая взвешенная рассчитывается по формуле:

 

Наиболее часто в статистике используется мода и медиана. Мода представляет собой значение изучаемого признака , повторяющегося с наибольшей частотой.

Медиана – это значение признака , приходящееся на середину ранжированной (упорядоченной) совокупности. Основное свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше чем от другой любой величины.

По сгруппированным данным мода определяется по таблице. Медианное значение признака рассчитывается по формуле:

, где п - объем совокупности.

В интервальном ряде мода рассчитывается по формуле:

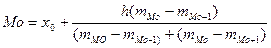
где, х₀ – нижняя граница модального интервала (интервала с наибольшей частотой), h – ширина модального интервала; мМо - частота модального интервала;

т_Мо-1 – частота интервала, предшествующего модальному;

т_Мо+1 – частота интервала, следующего за модальным.

 

В интервальном ряде медиана рассчитывается по формуле:

Где: x0 – нижняя граница медианного интервала (первый интервал, в котором накопленная частота превышает половину общей суммы частот); h – ширина медианного интервала; т_i - частота i-го интервала;

S_Мe-1 – накопленная частота интервала, предшествующего медианному;

т_Ме – частота медианного интервала.