Показатели вариации для характеристики вариационных рядов
Вариация означает колеблемость, изменчивость индивидуальных значений признака у отдельных единиц совокупности. Анализ показателей вариации позволяет оценить влияние факторов и условий производства на изменчивость признаков. Статистика, изучающая количественную сторону общественных явлений, всегда имеет дело с варьированием признаков. Так, варьируют выработка и заработная плата у отдельных работников, что вызвано различием уровней квалификации, образования, автоматизации производства, стажем работы и другими факторами. Вариацию характеризуют следующие показатели:
- размах вариации; - средние величины; - среднее линейное отклонение;
- среднее квадратическое отклонение; - дисперсия; - мода и медиана;
- асимметрия распределения и эксцесс;
- относительные показатели вариации (коэффициенты осцилляции, вариации, линейный коэффициент вариации).
Наиболее простой характеристикой вариации является размах вариации, который определяется как разность между наибольшим и наименьшим значениями варьирующего признака: R = xmax–xmin. Этот показатель дает самое общее представление о колеблемости признака, его значение определяется только двумя крайними значениями. Размах вариации предназначен для измерения колеблемости признаков в совокупностях с небольшой численностью единиц.
Для характеристики вариации необходимо знать не только размах значений признака, но и обобщенные (суммарные) отклонения всех значений признака от какого-то типичного для изучаемой совокупности значения. Наиболее распространенной формой статистических показателей является средняя величина.
4.3. Средние величины: определение; основное условие их применения; виды средних (простых и средневзвешенных). Правило мажорантности средних.
Изучаемые признаки колеблются (варьируют) с переходом от одной единицы к другой. С одной стороны, если рассчитать в каждой группе средний размер признака (среднюю численность работников, среднюю себестоимость и др.), то выяснится, что для каждой группы характерен свой средний размер показателей, отличный от размера аналогичных показателей в других типовых группах.
Свойства средней:
1. обнаруживать (улавливать) общую тенденцию изменения анализируемых показателей проявляется в результате объединения большого количества, массы индивидуальных величин. При расчете средней в массе индивидуальных величин их случайные отклонения взаимно погашаются и тогда обнаруживается тот типичный размер признака, который присущ всей совокупности единиц. Свойство средней величины улавливать общие тенденции и типичные черты однотипных явлений известно под именем закона больших чисел или закона средних чисел.Поэтому средние показатели выступают в качестве характеристики основных свойств и типичных размеров общественных явлений. На основе средних величин изучается уровень эффективности использования ресурсов, дается характеристика оплаты труда, потребления услуг связи, размера потребительской корзины.
2. основное свойство – быть обобщающей характеристикой качественно однородной совокупности, т.е. состоящей из индивидуальных величин одного и того же вида. Основным условием правильного применения средних величин в статистике является предварительная группировка изучаемых единиц. Если в изучаемом явлении выделены характерные типы и однородные группы единиц, тогда возможна их характеристика с помощью средних величин. Если совокупность неоднородна, то общие средние должны быть заменены и дополнены групповыми средними, т.е. средними, рассчитанными по качественно однородным группам.
В зависимости от характера первичных данных, области применения и способа расчета различают виды средних: средняя арифметическая, средняя гармоническая, средняя геометрическая и средняя квадратическая. Теория статистики указывает, какая средняя необходима в том или ином случае и как правильно ее рассчитывать.
Названные средние относятся к классу степенных. Общие формулы степенных средних имеют следующий вид:
простая 
, взвешенная 
,
где х – варианта, т.е. варьирующая, изменяющаяся величина признака; n – число единиц или объем совокупности (число вариантов); f – частота признака (вес I-того варианта); z – показатель степени средней.
Простая и взвешенная степенные средние – это средние одного и того же вида, но их исчисление зависит от исходных данных. Если исходные данные не систематизированы, применяется формула простой степенной средней. Если они сгруппированы и представлены вариационным рядом, используется формула взвешенной степенной средней.
Изменение значения показателя степени средней определяет ее вид:
| Наименование средней | Условноеобозначение | Значение | Формула средней | |
| простой | взвешенной | |||
| средняя гармоническая |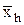 
| –1 | 
| 
|
| средняя геометрическая | 
| 
| 
| |
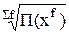
| средняя арифметическая |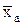 
| +1 | 
| 
|
| средняя квадратическая | 
| +2 | 
| 
|
П – знак умножения.
В зависимости от того, как образуется общий объем варьирующего признака, выбирают ту или иную среднюю: если объем признака образуется как сумма вариантов, то используется средняя арифметическая, если как сумма обратных значений – то средняя гармоническая, если как произведение вариантов – то средняя геометрическая, если как сумма квадратов значений признака – то средняя квадратическая.
Разные средние при одном и том же исходном материале имеют неодинаковое значение.
Например, имеются классы квалификации 1, 2, 3-й.
Исчислим средние:
гармоническая 
;
геометрическая 
;
арифметическая 
;
квадратическая 
В общем виде такое соотношение выглядит следующим образом:
xh<xq<xa<xk и называется правилом мажорантности средних. Оно представляется показателем степени; чем больше показатель степени в формуле средней, тем больше ее величина.
В статистике связи наиболее часто в расчетах прибегают к средней арифметической, поскольку она соответствует природе экономических явлений. При наличии данных о ценах (тарифах) на отдельные виды товаров (услуг) и общем объеме выручки от продажи (доходах от реализации услуг) для исчисления средних цен на продукцию (средних тарифов на услуги) используют среднюю гармоническую. Средняя геометрическая используется при расчетах показателей динамики, средняя квадратическая – показателей вариации.
В формуле средней арифметической взвешенной факт умножения варьирующего признака на частоту (вес) устанавливает долю каждого варианта в объеме признака или, другими словами, осуществляет взвешивание вариантов. С математической точки зрения средняя арифметическая взвешенная является наиболее общей формулой средней арифметической, а средняя арифметическая простая – частным случаем средней арифметической взвешенной, когда каждый вариант встречается только 1 или одинаковое количество раз.
Изменение средней при изменении вариантов является вполне естественным. Например, если заработная плата каждого рабочего цеха в отчетном периоде увеличилась, то увеличится и средняя заработная плата. А вот влияние на величину средней распределения весов, т.е. структуры изучаемой совокупности, не всегда очевидно. Таким образом, изменение весов признака меняет значение средней: если увеличивается удельный вес вариант с наибольшими значениями признака, то средняя растет; если же увеличивается удельный вес вариант с малыми значениями признака, то средняя уменьшается.
На практике часто приходится исчислять среднюю на основе интервального вариационного ряда. Например, данные о продолжительности междугородных телефонных соединений, как правило, выражаются интервальным вариационным рядом.
Если продолжительность разговора представлена не одним числом, а интервалом "от–до", то среднюю можно найти только приближенно. Предполагают, что внутри каждой группы значение признака распределяется равномерно и середина интервала служит для данной группы средним значением признака. Середина интервала исчисляется как средняя величина начального и конечного значений интервала.
Средняя арифметическая обладает рядом математических свойств:
1. Произведение средней на сумму частот всегда равно сумме произведений отдельных вариантов на соответствующие им частоты: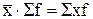 
.
Это свойство обусловлено сущностью средней арифметической, при исчислении которой уравнивание вариантов путем их замены средней величиной оставляет неизменным общий объем варьирующего признака.
2. Сумма отклонений индивидуальных значений признака от средней арифметической равно нулю: S(x–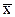
)f = 0.
3. Если все варианты значений признака уменьшить (увеличить) на какое-либо произвольное число А, то новая средняя арифметическая уменьшится (увеличится) на эту же величину:
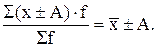
4. Если все варианты значений признака уменьшить (увеличить) в k раз, то новая средняя соответственно уменьшится (увеличится) в k раз:
; 
.
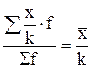5. Если все частоты (веса) уменьшить (увеличить) в k раз, то средняя арифметическая от этого не изменится:
.
6. Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем сумма квадратов их отклонений от любой другой произвольной величины С:
S(x–c)2f = S(x–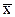)2f + S(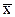–c)2f , т.е. S(x–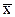)2f < S(x–c)2f на величину S(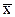–c)2f.
Свойства средней арифметической позволяют упростить её расчет: для этого можно вычесть из всех вариантов значений признака постоянное число, например, серединный вариант, разделить варианты на какую-либо величину (например, в рядах с равными интервалами на значение интервала), выразить частоты в процентах.
Вычисление средней арифметической с применением первых двух приемов называется способом отсчета от условного нуля:
,
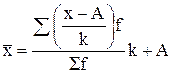где А – постоянное число; k – величина интервала.
Возможность определения средней величины по формуле как средней арифметической, так и средней гармонической видна и из преобразований формул этих средних: формула средней гармонической переходит в среднюю арифметическую и обратно. На самом деле, Sw – это сумма индивидуальных значений признака, его объем, т.е. Sxf. Подставив в формулу вместо Sw значение Sxf, получаем:
.
Мы пришли к формуле средней арифметической взвешенной.
С помощью средней гармонической в статистике связи рассчитываются также средние доходные таксы, средние затраты времени на выполнение операций и др
Средняя геометрическая применяется в тех случаях, когда изучаются не абсолютные показатели, а отношения двух величин. Поэтому она используется в анализе динамики при расчетах средних темпов роста, интегральных показателей как средних геометрических соотношений.
Средняя квадратическая используется главным образом в анализе вариации.
Характеристика вариации признака на основе отклонений его значений от средней может быть дана с помощью среднего линейного отклонения, рассчитываемого на основе абсолютных отклонений вариантов от их средней:l 
, 
.
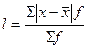Первая формула применяется для несистематизированных данных, вторая – в вариационных рядах. Необходимость обращения к модулю абсолютных значений отклонений (прямые скобки в числителе формулы) вызвана тем, что алгебраическая сумма этих отклонений равна нулю (свойство средней арифметической).
Большое применение в анализе вариации имеет способ расчета квадратов отклонений вариантов от их средней арифметической и последующим их усреднением. Такой способ расчета позволяет получить еще один показатель вариации – дисперсию.
Дисперсия представляет собой средний квадрат отклонений индивидуальных значений признака от их средней арифметической:
; 
.
Корень квадратный из дисперсии представляет собой среднее квадратическое отклонение:
; 
.
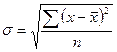Среднее квадратическое отклонение, как и среднее линейное отклонение, измеряет абсолютную меру колеблемости признака и выражается в тех же единицах измерения, что и варианты. В зарубежной статистической практике среднее квадратическое отклонение называется стандартным отклонением и применяется в различных стандартах.
Когда возникает необходимость измерения не только абсолютной вариации, но и относительной, то исчисляют относительные показатели вариации – коэффициенты вариации. Это, прежде всего, нужно для сравнения вариации признаков, измеряемых разными единицами, например: сравнить вариацию заработной платы в рублях, выработки в стоимостном и натуральном выражении, стажа работы в годах и разряда квалификации в коэффициентах. Коэффициент вариации представляет собой отношение размаха, среднего линейного или среднего квадратического отклонения к средней арифметической, выраженное в процентах или долях:
коэффициент осцилляции: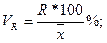 
линейный коэффициент вариации: 
коэффициент вариации: 