Показатели дифференциации и концентрации

Структуру вариационного ряда характеризуют значения признака, аналогичные медиане. Значения признака, которые делят все единицы распределения на равные численности, называются квантилями или градиентами. Частные случаи квантилей приведены на рис. 5.5.

Квантили используются для характеристики степени различия (однородности) значений уровней показателя вариационного ряда. На основании значений квантилей рассчитывают коэффициенты дифференциации (см. табл. 5.8), широко используемые при изучении дифференциации доходов населения.

Таблица 5.8

Общая характеристика коэффициентов дифференциации

Название показателя	Методика расчета	Сущностная характеристика
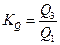
Квартильный коэффициент		характеризует соотношение между верхним и нижним квартилями и показывает во сколько раз минимальное значение признака в последней четверти единиц совокупности выше максимального значения признака в первой четверти единиц совокупности
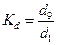
Децильный коэффициент		характеризует соотношение между верхним и нижним децилями. Применительно к статистике доходов населения: децильный коэффициент – показатель распределения доходов населения, характеризующий степень превышения минимального среднедушевого денежного дохода 10 % наиболее обеспеченной части населения над максимальным среднедушевым денежным доходом 10 % наименее обеспеченного населения
Коэффициент фондов (фондовый коэффициент)	*	определяется как соотношение между средними уровнями значений признака внутри сравниваемых групп, находящихся в разных концах ряда распределения. Он более точно измеряет уровень дифференциации

* Формула соответствует случаю, если ряд распределения разбит на десять частей, при этом 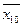и - соответственно среднее значение признака в десятой и первой частях ряда распределения.

* Второй квартиль (Q₂) равен медиане, а первый – Q₁ и третий Q₃ исчисляются аналогично расчету медианы, только вместо медианного интервала берется для первого квартиля интервал, в котором находится варианта, отсекающая ¼ численности частот, а для третьего квартиля – варианта, отсекающая ¾ частот.

, ,

где – нижняя граница интервала, содержащего нижний квартиль (интервал определяется по накопленной частоте, первой превышающей 25 %);

– нижняя граница интервала, содержащего верхний квартиль (интервал определяется по накопленной частоте, первой превышающей 75 %);

– величина интервала (квартильного);

– накопленная частота интервала, предшествующего интервалу, содержащему нижний квартиль;

– накопленная частота интервала, предшествующего интервалу, содержащему верхний квартиль;

– частота интервала, содержащего нижний квартиль;

– частота интервала, содержащего верхний квартиль.

^**Первый дециль d₁ делит совокупность в отношении 1 к 10, второй d₂ в соотношении 2 к 10 и т. д. Вычисляются они по той же схеме, что и медиана, и квартили, и квинтили.

, , и т.д.

d₁ – величина первого дециля, означающая, что 10 % единиц совокупности имеют значения ниже этого значения; d₉ - величина девятого дециля, означающая, что 10 % единиц совокупности имеют значения выше этого значения.

Рис. 5.5. Характеристика квантилей

К показателям дифференциации близки по значению показатели концентрации: коэффициент концентрации Джини, коэффициент Герфиндаля, коэффициент Розенблюта и др.

Коэффициент концентрации Джини (G) используют для характеристики степени неравномерности распределения значений признака вариационного ряда.

где p_i – накопленная частость (доля) численности единиц совокупности;

q_i – накопленная доля значений признака i-ой группы, приходящихся на все единицы совокупности ().

Коэффициент концентрации Джини может принимать значения от 0 до 1, поэтому результат следует разделить либо на 100, если p_i или q_i выражен в процентах, либо на 10000, если оба показателя выражены в процентах.

Удаление значения коэффициента Джини от нуля свидетельствует о возрастании степени неравномерности распределения значений признака в вариационном ряду и концентрации значений признака в отдельных группах.

Более простой показатель концентрации - коэффициент Герфиндаля(H), рассчитываемый на основе данных о доле суммарных значений признаков отдельных групп (выраженных, как правило, абсолютными величинами) в совокупном объеме значений признака.

где - доля значений признака i-ой группы в общем объеме значений признака.

Группами с незначительной долей значений признака можно пренебречь, так как, будучи возведенной в квадрат, такая доля выражается незначащим числом. Таким образом, значение коэффициента Герфиндаля определяется влиянием лишь доминирующих групп. Механизм расчета коэффициента Герфиндаля позволяет выделить доминирующие в совокупности группы, как наиболее весомые составляющие значения Н.

Основное достоинство коэффициента Герфиндаля – его высокая чувствительность к изменению в совокупном объеме долей наиболее крупных единиц совокупности, что позволяет отслеживать концентрацию значений признака. Другое достоинство данного коэффициента заключается в том, что он реагирует на число единиц в группе. Однако ее наибольшим значениям придается наибольший вес. Вследствие этого существует опасность преувеличения уровня концентрации. Поэтому наряду с коэффициентом Герфиндаля целесообразно применять коэффициент Розенблюта, который также характеризует концентрацию, однако расставляет акценты в обратном порядке: наибольший вес придается группам с наименьшими долями.

Коэффициент Розенблюта: ,

где i – номер группы в совокупности;

d_i – доля i-ой группы в общем объеме совокупности;

n- число групп в совокупности.

Диапазон значений коэффициента Розенблюта 0 ≤ K_R ≤ 1. При n = 1 и d₁ = 1 K_R = 1. В целом коэффициент Розенблюта имеет тенденцию преуменьшать концентрацию в совокупности.