Возведение в степень комплексных чисел в тригонометрической форме записи

Деление комплексных чисел в тригонометрической форме записи

Умножение комплексных чисел в тригонометрической форме записи

Действия с комплексными числами в тригонометрической форме записи

Пусть , , .

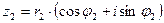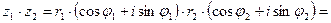
Итак,

,

Итак, ,

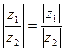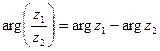
Примеры. Найти и 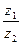, если , .

,

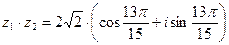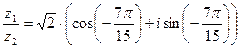
Определим понятие степени комплексного числа с целым показателем.

Определение. Степенью комплексного числа z с натуральным показателем n называется комплексное число, равное произведению n комплексных чисел, каждый из которых равен z.

.

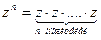По определению 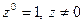, а .

, , …, .

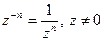– формула Муавра

Доказательство формулы Муавра проведите самостоятельно, используя метод математической индукции.

.

Таким образом, формула Муавра верна не только для целого положительного показателя, но и целого отрицательного.

Пример. Найти 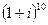. Запишем число в тригонометрической форме 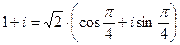. Теперь применим формулу Муавра .

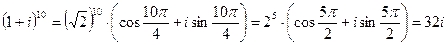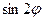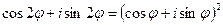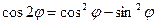Запишем формулу Муавра при r=1: . Эта формула дает возможность получить формулы для косинуса и синуса кратного угла. Например, получим формулы для и . или , откуда и . Самостоятельно получите формулы для и 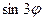.