Лекция 1

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

И УРАВНЕНИЯ, ДОПУСКАЮЩИЕ ПОНИЖЕНИЕ ПОРЯДКА

 

 

Дифференциальные уравнения произвольного и первого порядка

 

Определение 1. Дифференциальным уравнением называется соотношение, связывающее независимую переменную , искомую функцию и производные этой функции . В общем случае это соотношение можно записать в виде:

, (1)

где – некоторая функция переменных.

Порядком дифференциального уравнения называется наивысший порядок производной, входящей в это уравнение (т.е. формула (1) задает дифференциальное уравнение го порядка).

Решением (или частным решением) дифференциального уравнения (на некотором множестве) называется всякая функция , которая при подстановке в уравнение обращает его в тождество (на этом множестве).

Если решение уравнения задано в неявной форме , то такое равенство называют интегралом дифференциального уравнения.

График решения дифференциального уравнения называется интегральной кривой.

Решить дифференциальное уравнение – это означает найти все его решения.

Определение 2. Дифференциальным уравнением первого порядка называется уравнение

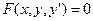, (2)

где – некоторая функция трех переменных. Если из этого уравнения можно выразить , то оно примет вид

, (3)

где – некоторая функция двух переменных. Уравнение (3) называется уравнением, разрешенным относительно производной.

Мы будем в основном рассматривать именно такие уравнения.

Определение 3.Задачей Коши для уравнения (13.3) называется задача

, (4)

где и – некоторые числа. Т.е. требуется найти решение дифференциального уравнения (3), удовлетворяющее начальному условию .