Линейные неоднородные уравнения с постоянными коэффициентами
Определение. Линейным неоднородным уравнением с постоянными коэффициентами называется уравнение вида:
 , ,
| (1) |
где  действительные числа.
действительные числа.
Например, уравнение II порядка будет выглядеть так:
 . .
| (2) |
Наша задача найти общее решение линейного неоднородного уравнения (1).
Запишем однородное уравнение, соответствующее (1):
 . .
| (3) |
Обозначим  общее решение уравнения (3), а через
общее решение уравнения (3), а через  какое-нибудь частное решение уравнения (1), тогда по теореме о структуре общего решения линейного неоднородного уравнения (п.14) решение уравнения (1) имеет вид:
какое-нибудь частное решение уравнения (1), тогда по теореме о структуре общего решения линейного неоднородного уравнения (п.14) решение уравнения (1) имеет вид:
 .
.
Как находить  мы знаем, следовательно, остается найти частное решение неоднородного уравнения. Иногда удается найти частное решение линейного неоднородного уравнения по виду правой части, т.е. по виду
мы знаем, следовательно, остается найти частное решение неоднородного уравнения. Иногда удается найти частное решение линейного неоднородного уравнения по виду правой части, т.е. по виду 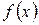 .
.
Рассмотрим линейное неоднородное уравнение II порядка с постоянными коэффициентами:
 . .
| (2) |
Случай I. Пусть правая часть уравнения (2) имеет вид
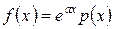 ,
,
где 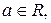
 многочлен степени п.
многочлен степени п.
Запишем однородное уравнение:
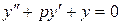 . .
| (4) |
Характеристическое уравнение

| (5) |
имеет два корня.
Справедливы следующие утверждения.
1) Если число а не является корнем характеристического уравнения (5), то частное решение уравнения (2) следует искать в виде:
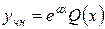 ,
,
где 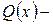 многочлен с неизвестными коэффициентами той же степени, что и
многочлен с неизвестными коэффициентами той же степени, что и  .
.
2) Если а – корень характеристического уравнения (5) (простой), то
 .
.
3) Если а – кратный корень уравнения (5), то
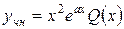 .
.
Предположим, что нам удалось установить вид частного решения уравнения (2). Оно содержит многочлен  с неизвестными коэффициентами, которые находятся методом уравнивания коэффициентов в левой и правой частях уравнения. Для этого находим производные
с неизвестными коэффициентами, которые находятся методом уравнивания коэффициентов в левой и правой частях уравнения. Для этого находим производные  и подставляем их вместе с самой функцией
и подставляем их вместе с самой функцией  в уравнение (2), получим тождество. Сокращая его на
в уравнение (2), получим тождество. Сокращая его на  , получим равенство двух многочленов: с одной стороны многочлен с неизвестными коэффициентами
, получим равенство двух многочленов: с одной стороны многочлен с неизвестными коэффициентами  , а с другой
, а с другой  . Приравнивая коэффициенты при одинаковых степенях, получим систему линейных уравнений, из которой найдем
. Приравнивая коэффициенты при одинаковых степенях, получим систему линейных уравнений, из которой найдем  .
.
Пример 1.  .
.
Решение.  .
.
1) Найдем  :
: 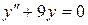 .
.
 корни комплексные, следовательно:
корни комплексные, следовательно:
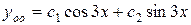 .
.
2)  будем искать в виде:
будем искать в виде:
 .
.
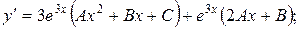

Все подставим в самое первое уравнение:
 ;
;
 .
.
Уравнивая коэффициенты, найдем А, В и С:
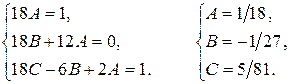
 .
.
 .
.
Ответ:  .
.
Случай II. Пусть правая часть уравнения (2) имеет вид:
 ,
,
где  многочлены.
многочлены.
Запишем однородное:

| (4) |
и характеристическое уравнения:
 . .
| (5) |
Имеют место следующие утверждения.
1) Если число  не корень (5), то
не корень (5), то  следует искать в виде:
следует искать в виде:

где  и
и  многочлены с неизвестными коэффициентами, степень каждого из которых равна наибольшей степени многочленов
многочлены с неизвестными коэффициентами, степень каждого из которых равна наибольшей степени многочленов  и
и  .
.
2) Если число  является корнем характеристического уравнения (5), то частное решение уравнения (2):
является корнем характеристического уравнения (5), то частное решение уравнения (2):
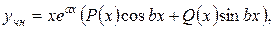
где  и
и  многочлены с неизвестными коэффициентами, степень каждого из которых равна наибольшей степени многочленов
многочлены с неизвестными коэффициентами, степень каждого из которых равна наибольшей степени многочленов  и
и  .
.
Коэффициенты в неизвестных многочленах  и
и  находятся методом неопределенных коэффициентов аналогично случаю 1.
находятся методом неопределенных коэффициентов аналогично случаю 1.
Замечание. Если правая часть уравнения (2) содержит только синус или косинус, то все равно частное решение  надо искать в вышеуказанном виде.
надо искать в вышеуказанном виде.
Пример 2.  .
.
Решение.
1) 

 .
.
2) Правая часть содержит косинус:
 .
.
Число  не является корнем характеристического уравнения, следовательно:
не является корнем характеристического уравнения, следовательно:
 .
.
Надо найти  :
:
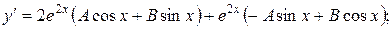


 .
.
Подставим в уравнение:


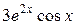 ;
;
 .
.

 .
.
 .
.
Ответ:  .
.