Линейное уравнение первого порядка
Определение. Линейным неоднородным уравнением первого порядка называется уравнение вида:  (2)
(2)
где  и
и  известные функции, непрерывные в некотором интервале
известные функции, непрерывные в некотором интервале 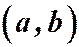 . Если
. Если  , то получим:
, то получим:  (3)
(3)
Уравнение (3) называется линейным однородным уравнением, соответствующим неоднородному уравнению (2).
Линейное однородное уравнение (3) является уравнением с разделяющимися переменными. Решим его:



 общее решение уравнения (3).
общее решение уравнения (3).
5.4. Метод Бернулли
Решение неоднородного уравнения (2) будем искать в виде произведений двух функций:  , где
, где  и
и  пока неизвестные функции.
пока неизвестные функции.
 .
.
Подставим в уравнение (2):  .
.
Сгруппируем слагаемые с и: .
.
Потребуем, чтобы выражение в скобках равнялось нулю и тогда уравнение распадается на два уравнения:  (4)
(4)
Из первого уравнения системы (4) найдем функцию v:




 .
.
Подставим найденную v во второе уравнение системы (4):
 ;
; 

Значит, общее решение уравнения (2) следующее:
 .
.
Пример 4.  линейное неоднородное уравнение.
линейное неоднородное уравнение.
Решение. Будем искать решение в виде  ,
,  .
.
 ;
; 





 .
.
Подставим  во второе уравнение системы:
во второе уравнение системы:

 ;
; 
 .
.
Ответ:  .
.