Скалярное умножение векторов
1. Определение и простейшие свойства. Возьмем ненулевые векторы а и b и отложим их от произвольной точки О: ОА = а и ОВ = b. Величина угла АОВ называется углом между векторами а и b и обозначается Ð(a,b). Если же хотя бы один из двух векторов – нулевой, то угол между ними по определению считается прямым. Заметим, что по определению угол между векторами не меньше 0 и не больше p. При этом угол между двумя ненулевыми векторами равен 0 тогда и только тогда, когда эти векторы сонаправлены и равен p тогда и только тогда, когда они противоположно направлены.
Проверим, что угол между векторами не зависит от выбора точки О. Это очевидно, если векторы коллинеарны. В противном случае отложим от произвольной точки О1 векторы О1А1 = а и О1В1 = b и заметим, что треугольники АОВ и А1О1В1 равны по трем сторонам, ибо |ОА| = |О1А1| = |а|, |ОВ| = |О1В1| = |b|, |АВ| = |А1В1| = |b–а|. Поэтому углы АОВ и А1О1В1 равны.
Теперь мы можем дать основное в этом параграфе
(5.1) Определение. Скалярным произведением двух векторов а и b (обозначается ab) называется число[6], равное произведению длин этих векторов на косинус угла между векторами. Короче:
ab = |a||b|cosÐ(a,b).
Операция нахождения скалярного произведения называется скалярным умножением векторов. Скалярное произведение аа вектора на себя называется скалярным квадратом этого вектора и обозначается а2.
(5.2) Скалярный квадрат вектора равен квадрату его длины.
ÿ Если |а| ¹0, то Ð(a,a) = 0, откуда а2 = |а||а|cos0 = |a|2. Если же а = 0, то а2 = |а|2 = 0. ÿ
(5.3) Неравенство Коши. Модуль скалярного произведения двух векторов не превосходит произведения модулей сомножителей: |ab| £ |a||b|. При этом равенство достигается тогда и только тогда, когда векторы а и b коллинеарны.
ÿ По определению |ab| = ||a||b|cosÐ(a,b)| = |a||b||cosÐ(a,b)| £ |a||b. Этим доказано само неравенство Коши. Теперь заметим. что для ненулевых векторов а и b равенство в нем достигается тогда и только тогда, когда |cosÐ(a,b)| = 1, т.е. при Ð(a,b) = 0 или Ð(a,b) = p. Последнее равносильно тому, что векторы а и b сонаправлены или противоположно направлены, т.е. коллинеарны. Если же хотя бы один из векторов а и b – нулевой, то они коллинеарны и |ab| = |a||b| = 0. ÿ
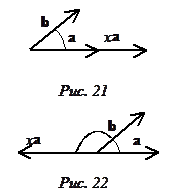 2. Основные свойства скалярного умножения. К ним относят следующие:
2. Основные свойства скалярного умножения. К ним относят следующие:
(СУ1) ab = ba (коммутативность);
(СУ2) (ха)b = х(ab) (ассоциативность);
(СУ3) а(b+c) = ab + ac (дистрибутивность).
Коммутативность здесь очевидна, ибо Ðab = Ðbа. Ассоциативность при х = 0 также очевидна. Если х > 0, то
(ха)b = |ха||b|cosÐ(хa,b) = |х||а||b|cosÐ(хa,b) = х|а||b|cosÐ(a,b) = х(ab),
ибо Ð(хa,b) = Ð(a,b) (из сонаправленности векторов ха и а – рис.21). Если же х < 0, то
(ха)b = |х||а||b|cosÐ(хa,b) = –х|а||b|(–cosÐ(a,b)) = х|а||b|cosÐ(a,b) = х(ab),
ибо Ð(хa,b) = p – Ð(a,b) (из противоположной направленности векторов ха и а – рис.22). Таким образом, ассоциативность тоже доказана.
Доказать дистрибутивность сложнее. Для этого нам потребуется такая
(5.4) Лемма. Пусть а – ненулевой вектор, параллельный прямой l, а b – произвольный вектор. Тогда ортогональная проекция b' вектора b на прямую l равна 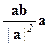 .
.
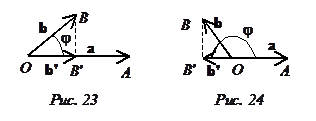 ÿ Если b = 0, то b' = 0 и ab = 0, так что в этом случае лемма верна. В дальнейшем будем считать, что вектор b' ненулевой. В этом случае от произвольной точки О прямой l отложим векторы ОА = а и ОВ = b, а также опустим перпендикуляр BB' из точки В на прямую l. По определению OB' = b' и Ð(a,b) = ÐАОВ. Обозначим ÐАОВ через j и докажем лемму отдельно для каждого из следующих трех случаев:
ÿ Если b = 0, то b' = 0 и ab = 0, так что в этом случае лемма верна. В дальнейшем будем считать, что вектор b' ненулевой. В этом случае от произвольной точки О прямой l отложим векторы ОА = а и ОВ = b, а также опустим перпендикуляр BB' из точки В на прямую l. По определению OB' = b' и Ð(a,b) = ÐАОВ. Обозначим ÐАОВ через j и докажем лемму отдельно для каждого из следующих трех случаев:
1) j < p/2. Тогда векторы а и 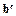 сонаправлены (рис.23) и
сонаправлены (рис.23) и
b' =  =
= 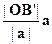 =
= .
.
2) j > p/2 . Тогда векторы а и b' противоположно направлены (рис.24) и
b' = – = –
= –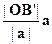 =
=  .
.
3) j = p/2. Тогда b' = 0 и ab = 0, откуда b' = 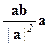 = 0. ÿ
= 0. ÿ
Теперь докажем дистрибутивность (СУ3). Она очевидна, если вектор а – нулевой. Пусть а ¹ 0. Тогда проведем прямую l || а, и обозначим через b' и c' ортогональные проекции на нее векторов b и с, а через d' – ортогональную проекцию на нее вектора d = b+c. По теореме 3.5 d' = b'+c'. Применяя к последнему равенству лемму 5.4, получаем равенство  =
=  . Скалярно умножив его на а, находим, что
. Скалярно умножив его на а, находим, что  2 =
2 =  , откуда ad = ab+ac, что и требовалось доказать. ÿ
, откуда ad = ab+ac, что и требовалось доказать. ÿ
Доказанные нами свойства скалярного умножения векторов аналогичны соответствующим свойствам умножения чисел. Но не все свойства умножения чисел переносятся на скалярное умножение векторов. Вот типичные примеры:
 1) Если ab = 0, то это не означает, что а = 0 или b = 0. Пример: два ненулевых вектора, образующие прямой угол.
1) Если ab = 0, то это не означает, что а = 0 или b = 0. Пример: два ненулевых вектора, образующие прямой угол.
2) Если ab = ac, то это не означает, что b = с, даже если вектор а – ненулевой. Пример: b и с – два различных вектора одинаковой длины, образующие с вектором а равные углы (рис. 25).
3) Неверно, что всегда а(bc) = (ab)c: хотя бы потому, что справедливость такого равенства при bc, ab ¹ 0 влечет коллинеарность векторов а и с.
3. Ортогональность векторов. Два вектора называются ортогональными, если угол между ними – прямой. Ортогональность векторов обозначается значком ^.
Когда мы определяли угол между векторами, то договорились считать угол между нулевым вектором и любым другим вектором прямым. Поэтому нулевой вектор ортогонален любому. Это соглашение позволяет доказать такой
(5.5) Признак ортогональности двух векторов. Два вектора ортогональны тогда и только тогда, когда их скалярное произведение равно 0.
ÿ Пусть а и b – произвольные векторы. Если хотя бы один из них – нулевой, то они ортогональны, а их скалярное произведение равно 0. Таким образом, в этом случае теорема верна. Допустим теперь, что оба данных вектора – ненулевые. По определению ab = |a||b|cosÐ(a,b). Поскольку по нашему предположению числа |a| и |b| не равны 0, то ab = 0 Û cosÐ(a,b) = 0 Û Ð(a,b) = p/2, что и требовалось доказать. ÿ
Равенство ab = 0 часто принимают за определение ортогональности векторов.
(5.6) Следствие. Если вектор а ортогонален каждому из векторов а1, …, ап, то он ортогонален и любой их линейной комбинации.
ÿ Достаточно заметить, что из равенства аа1 = … = аап = 0 следует равенство а(х1а1 + … +хпап) = х1(аа1) + … + хп(аап) = 0. ÿ
Из следствия 5.6 легко выводится школьный признак перпендикулярности прямой и плоскости. В самом деле, пусть некоторая прямая MN перпендикулярна двум пересекающимся прямым АВ и АС. Тогда вектор MN ортогонален векторам АВ и АС. Возьмем в плоскости АВС любую прямую DE. Вектор DE компланарен неколлинеарным векторам АВ и АС, и потому раскладывается по ним. Но тогда он тоже ортогонален вектору MN, то есть прямые MN и DE перпендикулярны. Получается, что прямая MN перпендикулярна любой прямой из плоскости АВС, что и требовалось доказать.
4. Ортонормированные базисы. (5.7) Определение. Базис векторного пространства называется ортонормированным, если, во-первых, все его векторы имеют единичную длину и, во-вторых, любые два его вектора ортогональны.
Векторы ортонормированного базиса в трехмерном пространстве обычно обозначают буквами i, j и k, а на векторной плоскости – буквами i и j. Учитывая признак ортогональности двух векторов и равенство скалярного квадрата вектора квадрату его длины, условия ортонормированности базиса (i,j,k) пространства V3 можно записать так:
(5.8) i2 = j2 = k2 = 1 , ij = ik = jk = 0,
а базиса (i,j) векторной плоскости – так:
(5.9) i2 = j2 = 1 , ij = 0.
Пусть векторы а и b имеют в ортонормированном базисе (i,j,k) пространства V3 координаты (а1, а2, а3) и (b1 b2, b3) соответственно. Тогда ab = (а1i+а2j+а3k)(b1i+b2j+b3k) = a1b1i2+a2b2j2+a3b3k2+a1b2ij+a1b3ik+a2b1ji+a2b3jk+a3b1ki+a3b2kj = a1b1 + a2b2 + a3b3. Так получается формула для скалярного произведения векторов а(а1,а2,а3) и b(b1,b2,b3), заданных своими координатами в ортонормированном базисе пространства V3:
(5.10) ab = a1b1 + a2b2 + a3b3.
Для векторов а(а1,а2) и b(b1, b 2), заданных своими координатами в ортонормированном базисе на векторной плоскости, она имеет вид
(5.11) ab = a1b1 + a2b2.
Подставим в формулу (5.10) b = a. Получится, что в ортонормированном базисе а2 = а12 + а22 + а32 . Поскольку а2 = |а|2 , получается такая формула для нахождения длины вектора а(а1,а2,а3), заданного своими координатами в ортонормированном базисе пространства V3 :
(5.12) |а| =  .
.
На векторной плоскости она в силу (5.11) приобретает вид
(5.13) |а| =  .
.
Подставляя в формулу (5.10) b = i, b = j, b = k, получаем еще три полезных равенства:
(5.14) ai = a1, aj = а2, ak = а3.
Простота координатных формул для нахождения скалярного произведения векторов и длины вектора составляет главное преимущество ортонормированных базисов. Для неортонормированных базисов эти формулы, вообще говоря, неверны, и их применение в этом случае является грубой ошибкой.
5. Направляющие косинусы. Возьмем в ортонормированном базисе (i,j,k) пространства V3 вектор а(а1,а2,а3). Тогда ai = |a||i|cosÐ(a,i) = |a|cosÐ(a,i). С другой стороны, ai = a1по формуле 5.14. Получается, что
(5.15) а1 = |a|cosÐ(a,i).
и, аналогично,
а2 = |a|cosÐ(a,j), а3 = |a|cosÐ(a,k).
Если вектор а – единичный, эти три равенства приобретают особенно простой вид:
(5.16) а1 = cosÐ(a,i), а2 = cosÐ(a,j), а3 = cosÐ(a,k).
Косинусы углов, образованных вектором с векторами ортонормированного базиса, называются направляющими косинусами этого вектора в данном базисе. Как показывают формулы 5.16, координаты единичного вектора в ортонормированном базисе равны его направляющим косинусам.
Из 5.15 вытекает, что а12 + а22 + а32 = |а|2(cos2Ð(a,i)+cos2Ð(a,j) +cos2Ð(a,k)). С другой стороны, а12 + а22 + а32 = |а|2. Получается, что
(5.17) сумма квадратов направляющих косинусов ненулевого вектора равна 1.
Этот факт бывает полезен для решения некоторых задач.
(5.18) Задача. Диагональ прямоугольного параллелепипеда образует с двумя его ребрами, выходящими из той же вершины, углы по 60°. Какой угол она образует с третьим выходящим из этой вершины ребром?
ÿ Рассмотрим ортонормированный базис пространства V3, векторы которого изображены ребрами параллелепипеда, выходящим из данной вершины. Поскольку вектор диагонали образует с двумя векторами этого базиса углы по 60°, квадраты двух из трех его направляющих косинусов равны cos260° = 1/4. Поэтому квадрат третьего косинуса равен 1/2, а сам этот косинус равен 1/ . Значит, искомый угол равен 45°. ÿ
. Значит, искомый угол равен 45°. ÿ