Координаты вектора.

Векторные пространства.

1. Векторные пространства. Совокупность векторов V называется векторным пространством, если она непуста и обладает следующими двумя свойствами:

(V1) Сумма любых двух векторов из V содержится в V (замкнутость относительно сложения).

(V2) Произведение вектора из V на любое число содержится в V (замкнутость относительно умножения вектора на число).

Два этих условия можно заменить одним:

(V) Любая линейная комбинация векторов из V содержится в V.

ð В самом деле, если выполнено условие (V), то вместе с любыми векторами a и b совокупность V содержит векторы xa для любого числа х и a+b = 1a+1b. Обратно, если выполнены условия (V1) и (V2), то в любой линейной комбинации векторов из V входят в V все слагаемые (в силу (V2)), а вместе с ними – и вся комбинация (в силу (V1)). ð

Возьмем любой вектор а из векторного пространства V и умножим его на нуль. В силу условия (V2) получившееся произведение тоже должно содержаться в пространстве V. Получается, что всякое векторное пространство содержит нулевой вектор. Простейшим примером векторного пространства служит совокупность, состоящая из одного нулевого вектора. Такое векторное пространство называется нулевым. Другой очевидный пример векторного пространства – совокупность всех векторов.

Рассмотрим менее очевидные примеры. Пусть V(p) есть совокупность всех векторов, параллельных данной прямой р. Она непуста, а условия (V1) и (V2) выполнены для нее в силу леммы 2.14. Таким образом V(p) есть векторное пространство. Оно называется векторной прямой. По тем же причинам векторным пространством является векторная плоскость V(П) – совокупность всех векторов, параллельных данной плоскости П. Ясно, что две векторные прямые (плоскости) совпадают, когда задающие их прямые (плоскости) параллельны и не совпадают в противном случае.

Можно показать, что других видов векторных пространств, кроме перечисленных выше, нет[5].

2. Базис векторного пространства. Базисом пространства всех векторов называется любая упорядоченная тройка некомпланарных векторов. Базисом векторной плоскости V(П) называется любая упорядоченная пара неколлинеарных векторов этой плоскости. Базисом векторной прямой V(р) называется любой ее ненулевой вектор.

(4.1) Основное свойство базиса (ОСБ). Всякий вектор, принадлежащий векторному пространству, можно разложить по любому базису этого пространства и притом только одним способом.

ÿ Проверим ОСБ отдельно для каждого из видов векторных пространств.

1) Возьмем любой ненулевой вектор а из векторной прямой V(р). Все векторы из V(р) коллинеарны ему. Значит, все их можно разложить по нему в силу теоремы 3.7. Допустим, что нашелся вектор р, который выражается через а двумя способами: р = ха и р = уа. Вычитая, получаем 0 = (х–у)а. Так как вектор а – ненулевой, то х–у = 0, т.е. х = у. Это доказывает единственность разложения вектора р по базису (а) векторной прямой.

2) Пусть а и b – неколлинеарные векторы, принадлежащие векторной плоскости V(П). Возьмем любой вектор р из этой векторной плоскости. Векторы а, b и р параллельны одной плоскости П, поэтому вектор р можно разложить по векторам а и b (теорема 3.10). Допустим, нашлись два разложения: р = ха+уb и р = zа+tb. Вычитая эти равенства, получаем 0 = (x–z)а+(y–t)b (*). Допустим, что x ¹ z. Тогда x–z ¹ 0, и мы можем в равенстве (*) выразить вектор а через вектор b: 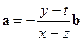. Но это противоречит неколлинеарности векторов а и b. Значит, x = z. Аналогично y = t. Это доказывает единственность разложения вектора р по базису (а,b) векторной плоскости.

3) Пусть а, b и с – некомпланарные векторы. В силу теоремы 3.12 по ним можно разложить любой вектор. Пусть какой-то вектор р удалось разложить по базису (а,b,с) пространства V3 двумя способами: р = ха+уb+uc и р = zа+tb+vc. Вычитая эти равенства, получаем 0 = (x–z)а+(y–t)b+(u–v)c (**).Допустим, что x ¹ z. Тогда мы сможем в равенстве (**) выразить вектор а через векторы b и с: 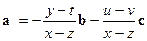. Но это означает, что векторы а, b и с компланарны, что противоречит условию. Значит, x = z. Аналогично y = t и u = v. Это доказывает единственность разложения вектора р по базису (а,b,с). ÿ

Количество векторов в базисе векторного пространства называется его размерностью. Размерность векторной прямой равна единице, векторной плоскости – двум, а пространства всех векторов – трем. Поэтому пространство всех векторов часто обозначается V3 и называется трехмерным векторным пространством, а векторные плоскости и прямые называются двумерными и одномерными векторными пространствами.

3. Координаты вектора в базисе. Пусть в векторном пространстве V выбраны базис B=(а1,...,ап) и вектор р. Разложим вектор р по базису B: р = х1а1 + ... + хпап (*). Коэффициенты х1, ..., хп называются координатами вектора р в базисе B. Из ОСБ следует, что каждый вектор пространства V имеет однозначно определенные координаты в любом данном базисе этого пространства. Ясно, что при этом число координат вектора равно числу векторов в базисе, т.е. размерности векторного пространства V.

Если вектор р имеет координаты х1,...,хп в базисе B, то пишут р = (х1,...,хп)B или, короче, р(х1,...,хп)B. Если по смыслу сказанного ясно, в каком базисе взяты координаты, пишут просто р(х1,...,хп). Иногда координаты вектора пишут не в строчку, а в столбик.

Координаты пишутся в том же порядке, в каком идут векторы базиса. Это позволяет с помощью формулы (*) однозначно восстановить вектор р по его координатам. Следовательно, если два вектора имеют в некотором базисе одинаковые наборы координат, то эти векторы равны. Поскольку координаты вектора в данном базисе определены единственным образом, верно и обратное: если два вектора равны, то равны и их координаты в данном базисе. Соединяя два эти утверждения, получаем

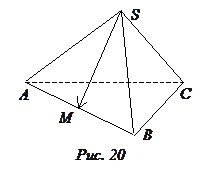(4.2) Координатный признак равенства двух векторов. Два вектора из одного и того же векторного пространства равны тогда и только тогда, когда равны их координаты в данном базисе этого пространства. Иначе говоря, если р=(х1,...,хп)B и q(у1,...,уп)B , то одно векторное равенство p = q равносильно системе из п числовых равенств: х1 = у1, ..., хп = уп. ÿ

Рассмотрим пример. Пусть точка М – середина ребра АВ треугольной пирамиды SABC (рис.20). Возьмем векторную плоскость V, составленную из всех векторов, параллельных плоскости SAB, а в ней – базис B = (SA, SB). Поскольку SM = 0,5SA + 0,5SB, вектор SM имеет в базисе B координаты (0,5; 0,5). Возьмем теперь базис B1 = (SA, SB, SC) в пространстве V3. Разложение вектора SM по нему имеет вид SM = 0,5SA + 0,5SB + 0SC. Поэтому в базисе B1 координаты вектора р равны (0,5, 0,5, 0). Если же взять в пространстве V3 базис B2 = (SA, SC, SB), то в нем координаты вектора р будут равны (0,5, 0, 0,5).

4. Поведение координат при операциях над векторами.

(4.3) Теорема. При сложении векторов их одноименные координаты в данном базисе тоже складываются. Если умножить вектор на число, то все его координаты умножатся на это число.

ÿ Возьмем для определенности базис B = (а, b) векторной плоскости V. Пусть в этом базисе вектор р имеет координаты (х1,у1), а вектор q – координаты(х2,у2). По определению это означает, что p = х1a + y1b, а q = х2a + y2b. Сложив эти равенства, получаем, что p + q = (х1+х2)a + (y1+y2)b, а это и означает, что сумма p+q имеет в базисе B координаты х1+ х2 и y1 + y2 . Умножим теперь равенство p = х1a+y1b на число х. Получим хр = хх1a+хy1b , т.е. координаты вектора хр в базисе B равны хх1 и ху1.

Мы доказали теорему для случая векторной плоскости. Для случаев векторной прямой и пространства всех векторов рассуждения аналогичны, как и для случая, когда складывается больше двух векторов. ÿ

 
Из доказанной теоремы вытекает такой

(4.4) Координатный признак коллинеарности двух векторов. Пусть два вектора заданы своими координатами в одном и том же базисе. Тогда коллинеарность этих векторов равносильна пропорциональности их координат.

ÿ Для определенности допустим, что базис взят в пространстве V3, и векторы а и b имеют в нем координаты (х1,у1,z1) и (х2,у2,z2) соответственно. Коллинеарность векторов а и b по признаку 2.13 равносильна тому, что один из них выражается через другой. Не умаляя общности, можно считать, что b = ха. По теореме 4.3 ха = (хх1,ху1,хz1). По признаку 4.2 векторное равенство а = хb равносильно системе из трех числовых:

(4.5) х2 = хх1 , у2 = ху1 , z2 = хz1.

Но она как раз и означает пропорциональность тройки чисел (х2,у2,z2) тройке (х1,у1,z1). ÿ

Если х1, у1, z1 ¹ 0, систему 4.5 можно записать в виде тройного равенства:

(4.6) ,

где каждая из дробей равна коэффициенту пропорциональности х. Если координаты берутся не в пространстве V3, а на векторной плоскости, то система 4.5 приобретает вид х2 = хх1 , у2 = ху1, а тройное равенство 4.6 (при х1, у1 ¹ 0) превращается в двойное: