Пучок прямых на плоскости
Определение 24. Пучком прямых на плоскости называется множество всех прямых этой плоскости, проходящих через одну точку. Эта точка называется центром пучка.
Пучок можно задать двумя способами: центром и парой пересекающихся прямых.
I.Пучок задан центром.
Дано.R =  , С(х0, у0) – центр пучка (рис. 28).
Найти условие, определяющее пучок.
Решение. Прямая l принадлежит пучку с центром С тогда и , С(х0, у0) – центр пучка (рис. 28).
Найти условие, определяющее пучок.
Решение. Прямая l принадлежит пучку с центром С тогда и
| 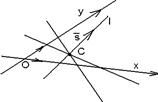 Рис. 28
Рис. 28
|
только тогда, когда l ' С. При этом направляющим вектором может быть любой ненулевой вектор  . Следовательно, l принадлежит пучку Û l :
. Следовательно, l принадлежит пучку Û l :  , где m, n – любые действительные числа, не равные одновременно нулю. Итак, пучок с центром С задаётся уравнением
, где m, n – любые действительные числа, не равные одновременно нулю. Итак, пучок с центром С задаётся уравнением  (36).
(36).
В уравнении (36) две пары переменных. Меняя m, n, мы будем получать все возможные прямые пучка. Если m, n зафиксированы, то зафиксирована прямая пучка. При этом, меняя х, у, мы будем получать все возможные точки на полученной прямой.
II. Пучок задан парой пересекающихся прямых.
Дано.R =  , l1 : A1x + B1y + C1 = 0, l2 : A2x + B2y + C2 = 0 (рис. 29).
Найти уравнение пучка.
Решение. Пусть l1 Ç l2 = С и С(х0, у0). Точка С будет центром пучка. Используя уравнение (36) получим, что прямая l принадлежит пучку Û l : , l1 : A1x + B1y + C1 = 0, l2 : A2x + B2y + C2 = 0 (рис. 29).
Найти уравнение пучка.
Решение. Пусть l1 Ç l2 = С и С(х0, у0). Точка С будет центром пучка. Используя уравнение (36) получим, что прямая l принадлежит пучку Û l :  . Здесь . Здесь
| 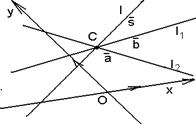 Рис. 29
Рис. 29
|
вектор  - любой ненулевой вектор. Из уравнений прямых l1 и l2 векторы
- любой ненулевой вектор. Из уравнений прямых l1 и l2 векторы 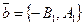 и
и 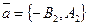 параллельны прямым l1 и l2 соответственно, поэтому они не коллинеарны. Следовательно, любой вектор
параллельны прямым l1 и l2 соответственно, поэтому они не коллинеарны. Следовательно, любой вектор 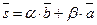 , где a, b - любые действительные числа, не равные нулю одновременно. Отсюда
, где a, b - любые действительные числа, не равные нулю одновременно. Отсюда 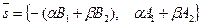 . Уравнение (36) перепишется
. Уравнение (36) перепишется 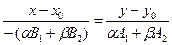 . После преобразования получим:
. После преобразования получим:
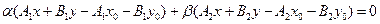 (*).
(*).
Так как С = l1 Ç l2, то A1x0 + B1y0 + C1 = 0 и A2x0 + B2y0 + C2 = 0. Отсюда -( A1x0 + B1y0) = С1, -( A2x0 + B2y0) = 0. Подставив в (*), получим уравнение данного пучка
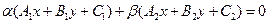 (37)
(37)
В уравнении (37) тоже две пары переменных (a, b) и (х, у).
Задача. Дано: R =  , l1 : 3х + 4у +12 = 0, l2 : 4х + 3у - 24 = 0, l3 : х + 2у + 3 = 0.
, l1 : 3х + 4у +12 = 0, l2 : 4х + 3у - 24 = 0, l3 : х + 2у + 3 = 0.
Найти уравнение прямой l, Если l ' (l1 Ç l2) и l ^ l3.
Решение. Так как l ' (l1 Ç l2), то l принадлежит пучку прямых, определяемому прямыми l1 и l2. Следовательно, уравнение l можно искать в виде
a(3х + 4у +12 ) + b(4х + 3у - 24) = 0 (*)
Преобразовав это уравнение, получим (3a + 4b)х + (4a +3b)у + (12a - 24b) = 0 (**).
Используем условие перпендикулярности прямых (33). Получим 1×(3a + 4b) + 2×(4a +3b) = 0, или 11a + 10b = 0. Так как все решения этого уравнения пропорциональны, а уравнение (*) при пропорциональных парах (a, b) задаёт одну и ту же прямую, то достаточно найти одну ненулевую пару (a, b). При a = 10 b = -11. Подставив в (**), получим уравнение
l : 14х - 4у - 384 = 0.
2.5. Геометрический смысл неравенств Ах + Ву + С ³ 0 (£ 0, >0, < 0)
Дано. R =  , Ах + Ву + С ³ 0 (А и В н равны нулю одновременно) (38).
, Ах + Ву + С ³ 0 (А и В н равны нулю одновременно) (38).
Исследовать, какую фигуру задаёт неравенство (38).
Решение. Пусть l : Ах + Ву + С = 0. Если бы вектор 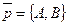 был параллелен прямой l, то векторы был параллелен прямой l, то векторы 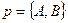 и и  были бы коллинеарны. Но тогда были бы коллинеарны. Но тогда  . Отсюда А2 + В2 = 0, т.е. . Отсюда А2 + В2 = 0, т.е.
| 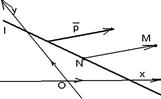 Рис. 30
Рис. 30
|
А = В = 0, что противоречит условию. Итак, вектор 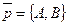 не параллелен прямой (рис.30).
не параллелен прямой (рис.30).
Рассмотрим множество всех точек плоскости, не лежащих на прямой l. Пусть М – любая из них. Пусть 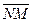 параллелен
параллелен 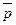 , где N Î l. Тогда
, где N Î l. Тогда 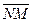 =
= 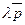 . При этом l > 0 Û точки М лежат в одной открытой полуплоскости с границей l, а именно в той в сторону которой направлен вектор
. При этом l > 0 Û точки М лежат в одной открытой полуплоскости с границей l, а именно в той в сторону которой направлен вектор 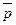 . Перепишем последнее равенство в координатах. Если М (х, у), N (х0 , у0), то х - х0 = lА, у - у0 = lВ. Отсюда х0 = х - lА, у0 = у - lВ. Так как N Î l, то Ах0 + Ву0 + С = 0. Следовательно, А(х - lА) + В(у - lВ) + С = 0. Отсюда Ах + Ву + С = l (А2 + В2). Так как А2 + В2 > 0, то знак трёхчлена Ах + Ву + С совпадает со знаком l . Итак, Ах + Ву + С > 0 Û точка М (х, у) лежит в открытой полуплоскости с границей l, а именно в той в сторону которой направлен вектор
. Перепишем последнее равенство в координатах. Если М (х, у), N (х0 , у0), то х - х0 = lА, у - у0 = lВ. Отсюда х0 = х - lА, у0 = у - lВ. Так как N Î l, то Ах0 + Ву0 + С = 0. Следовательно, А(х - lА) + В(у - lВ) + С = 0. Отсюда Ах + Ву + С = l (А2 + В2). Так как А2 + В2 > 0, то знак трёхчлена Ах + Ву + С совпадает со знаком l . Итак, Ах + Ву + С > 0 Û точка М (х, у) лежит в открытой полуплоскости с границей l, а именно в той в сторону которой направлен вектор 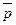 . Неравенство Ах + Ву + С ³ 0 задаёт эту полуплоскость вместе с границей.
. Неравенство Ах + Ву + С ³ 0 задаёт эту полуплоскость вместе с границей.