Расстояние от точки до прямой
Дано: R =  , l : Ax + By + C = 0, М0(х0, у0).
Найти d (M0, l ).
Решение. Опустим из точки М0 на данную прямую перпендикуляр. Пусть N – его основание и N(х1,у1). Тогда Ax1 + By1 + C = 0 (*). Искомое расстояние d (M0, l ) = , l : Ax + By + C = 0, М0(х0, у0).
Найти d (M0, l ).
Решение. Опустим из точки М0 на данную прямую перпендикуляр. Пусть N – его основание и N(х1,у1). Тогда Ax1 + By1 + C = 0 (*). Искомое расстояние d (M0, l ) =  . . Если Если  , то , то  . Следовательно, векторы . Следовательно, векторы 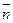 и и  коллинеарны. Так как коллинеарны. Так как 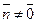 , то , то  (**). Отсюда следует (**). Отсюда следует
|  Рис. 26
Рис. 26
|
d (M0, l ) =  =
=  . (***)
. (***)
Для решения задачи достаточно найти  . Для этого обе части равенства (**) умножим скалярно на вектор
. Для этого обе части равенства (**) умножим скалярно на вектор 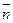 , получим
, получим  . Полученное равенство перепишем в координатах: А(х0 - х1) + В(у0 - у1) = d× (А2 + В2). Отсюда Ах0 + Ву0 - (Ах1 + Ву1) = d× (А2 + В2). Из (*) Ах1 + Ву1 = С. Следовательно, Ах0 + Ву0 + С = d× (А2 + В2) и
. Полученное равенство перепишем в координатах: А(х0 - х1) + В(у0 - у1) = d× (А2 + В2). Отсюда Ах0 + Ву0 - (Ах1 + Ву1) = d× (А2 + В2). Из (*) Ах1 + Ву1 = С. Следовательно, Ах0 + Ву0 + С = d× (А2 + В2) и  . Подставив в (***), получим d (M0, l ) =
. Подставив в (***), получим d (M0, l ) =  (35)
(35)
Задача.Дано: R =  , l1 : 3х + 4у +12 = 0, l2 : 4х + 3у - 24 = 0.
Найти уравнения биссектрис углов, образованных l1 и l2.
Решение. Пусть р1 и р2 – искомые биссектрисы. Тогда
М Î р1 или р2 Û d1 = d2,
где d1 = d (M, l1), d2 = d (M, l2 ). Используя формулу (35), получим
М Î р1 или р2 Û , l1 : 3х + 4у +12 = 0, l2 : 4х + 3у - 24 = 0.
Найти уравнения биссектрис углов, образованных l1 и l2.
Решение. Пусть р1 и р2 – искомые биссектрисы. Тогда
М Î р1 или р2 Û d1 = d2,
где d1 = d (M, l1), d2 = d (M, l2 ). Используя формулу (35), получим
М Î р1 или р2 Û  . .
|  Рис.27
Рис.27
|
После упрощения получим два уравнения:
р1 : х - у - 36 = 0; р2 : 7х + 7у - 12 = 0.
(Сравните с решением и результатом предыдущей задачи).