Смешанное произведение векторов
Определение 22. Смешанным произведением упорядоченной тройки векторов называется результат векторного произведения первых двух векторов, умноженный скалярно на третий вектор.
Если дана упорядоченная тройка векторов 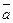 ,
, 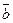 и
и  , то смешанным произведением будет число, равное
, то смешанным произведением будет число, равное  .
.
Свойства смешанного произведения векторов.
10. Смешанное произведение любой упорядоченной тройки векторов определено и однозначно.
20. Очевидно, смешанное произведение обладает всеми свойствами, общими для векторного и скалярного произведений. Так, например,  ,
,
 )×
)× ,
,  ,
,
 ,
,  ,
,  .
.
30. Смешанное произведение трёх векторов равно нулю тогда и только тогда, когда данные векторы компланарны.
Доказательство.  = 0 Û
= 0 Û  =
= 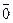 , или
, или  , или
, или  .
.
Но  =
= 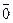 Û
Û 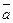 и
и 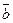 коллинеарны;
коллинеарны;  Û
Û  параллелен плоскости векторов
параллелен плоскости векторов 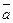 и
и 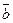 .
.
Следовательно,  = 0 Û
= 0 Û 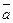 ,
, 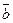 и
и  компланарны.
компланарны.
40. (Смешанное произведение в координатах).
Доказательство. Пусть В =  -ортонормированный базис,
-ортонормированный базис,  ,
,  ,
,  . Так как
. Так как  =
=  =
=  . Так как базис ортонормированный, то по формуле (7) получим
. Так как базис ортонормированный, то по формуле (7) получим
 =
=  (11)
(11)
50. Если в смешанном произведении поменять местами два множителя, то оно сменит знак.
Доказательство. Зафиксируем ортонормированный базис. Тогда смешанное произведение можно найти по формуле (11). Если два множителя в смешанном произведении меняются местами, то в определителе формулы (11) меняются местами две строки. При этом определитель меняет знак на противоположный.
60. Если в смешанном произведении все множители поменять местами, то смешанное произведение не изменится. (Докажите)
70. Смешанное произведение не изменится, если в нём поменять местами знаки векторного и скалярного умножения, т.е.  =
= 
Доказательство. Зафиксируем ортонормированный базис. Тогда  =
=  =
=  =
=  =
=  .
.
Замечание. Последнее свойство позволяет в обозначении смешанного произведения не ставить знаки векторного и скалярного произведений, поэтому смешанное произведение можно обозначать  .
.
80. Геометрический смысл модуля и знака смешанного произведения.
Если векторы компланарны, то смешанное произведение их равно нулю (свойство 30), поэтому рассмотрим упорядоченную тройку 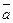 ,
, 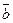 и
и  некомпланарных векторов. Отложим
некомпланарных векторов. Отложим
векторы 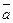 , , 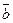 и и  от одной точки: от одной точки:  , ,  , ,  . Построим параллелепипед OADBCMNP на векторах . Построим параллелепипед OADBCMNP на векторах  , как на рёбрах. Пусть , как на рёбрах. Пусть  есть векторная проекция вектора есть векторная проекция вектора  на направление вектора на направление вектора  . Тройка векторов . Тройка векторов 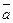 , , 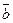 и и  всегда правая. Если тройка всегда правая. Если тройка 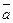 , , 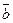 и и  тоже правая, то тоже правая, то  сонаправлен с вектором сонаправлен с вектором  , следовательно, числовая проекция , следовательно, числовая проекция  > 0 (рис. 24). Если > 0 (рис. 24). Если
|  Рис. 24
Рис. 24
|
же тройка 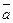 ,
, 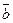 ,
,  левая, то
левая, то  противоположно направлен с вектором
противоположно направлен с вектором  , следовательно, числовая проекция
, следовательно, числовая проекция  < 0. Так как
< 0. Так как  =
=  , то знак
, то знак  совпадает со знаком
совпадает со знаком  . Итак,
. Итак,  > 0 Û тройка векторов
> 0 Û тройка векторов 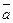 ,
, 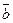 ,
,  правая и
правая и  < 0 Û тройка векторов
< 0 Û тройка векторов 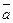 ,
, 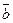 ,
,  левая.
левая.
½ ½=
½=  =
=  , где
, где  - высота параллелепипеда. Следовательно, ½
- высота параллелепипеда. Следовательно, ½ ½ =
½ =  , где
, где  - объём параллелепипеда OADBCMNP.
- объём параллелепипеда OADBCMNP.
90.  (формула для нахождения высоты параллелепипеда).
(формула для нахождения высоты параллелепипеда).
100. Если АВСD - тетраэдр, то  ,
,  .
.
Задача 11. АВСDA1B1C1D1 - куб с единичным ребром,  ,
,  ,
,
 , ,  . Найдите высоту тетраэдра MNPQ, опущенную из вершины Q.
Решение. . Найдите высоту тетраэдра MNPQ, опущенную из вершины Q.
Решение.  , ,  , ,  .
Выберем базис В = .
Выберем базис В =  , где , где  , ,  , ,  . Этот базис . Этот базис
|  Рис. 25
Рис. 25
|
ортонормированный. Найдём координаты векторов:  ,
,  ,
,
 . Следовательно,
. Следовательно,  ,
,
 ,
,  .
.
 =
=  ,
,  . Следовательно,
. Следовательно,
 .
.