Ортогональная проекция вектора на ось

Определение 15. Проектирование называется ортогональным, Если плоскость П ортогональна оси.

При ортогональном проектировании достаточно из данной точки опустить на ось перпендикуляр.

Теорема 2. Числовая ортогональная проекция вектора на ось равна произведению длины этого вектора на косинус его угла с осью.

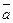Доказательство. Пусть l – ось, - её орт, - произвольный вектор. Если , то пр_l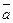= 0, поэтому можно считать, что утверждение теоремы верно. Пусть 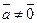и a = (l).

Возможны следующие случаи. 1) a = 0. В этом случае (рис. 14а) и пр= . 2) 0 < a < 900. В этом случае

Рис. 14 а)

Рис. 14 б)

(рис. 14б) , пр.

Рис. 14 в)

Рис. 14 г)

Рис. 14 д)

3) a = 90⁰ (рис. 14в). В этом случае пр= 0 и, следовательно, пр= .

4) 90⁰ < a < 180⁰ (рис. 14г). В этом случае , пр.

5) a = 180⁰ (рис. 14д). В этом случае пр= .

Итак, во всех случаях пр.