Базис векторного пространства. Координаты вектора
Пусть V – любое векторное пространство.
Определение 11.Базисом векторного пространства называется любая упорядоченная максимальная линейно независимая система его векторов.
(Обратите внимание: если система векторов  является максимальной линейно независимой, то системы
является максимальной линейно независимой, то системы  ;
;  ;
;  являются различными базисами.)
являются различными базисами.)
Примеры.
1. Во множестве всех геометрических векторов базисом является любая упорядоченная тройка некомпланарных векторов.
2. Во множестве всех компланарных векторов базисом является любая упорядоченная пара неколлинеарных векторов.
3. Во множестве всех коллинеарных векторов базисом является любой ненулевой вектор.
4. Векторное пространство, состоящее из одного нулевого вектора, не имеет базиса.
Определение 12. Число векторов в базисе векторного пространства называется размерностью этого пространства.
Следовательно, множество всех геометрических векторов есть трёхмерное векторное пространство. Множество всех компланарных векторов – двумерное векторное пространство. Множество всех коллинеарных векторов – одномерное векторное пространство.
Определение 13.Координатами вектора в данном базисе называется упорядоченный набор коэффициентов, с помощью которых этот вектор выражается через базисные векторы.
Пусть е =  - базис и
- базис и  . Упорядоченный набор {х, у, z} - это координаты вектора
. Упорядоченный набор {х, у, z} - это координаты вектора 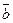 в базисе е. Обозначение
в базисе е. Обозначение 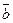 = {х, у, z}. Если используется несколько базисов, то обозначают
= {х, у, z}. Если используется несколько базисов, то обозначают 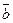 = {х, у, z}е.
= {х, у, z}е.
Задача 5. Пусть АВСD – параллелограмм,  ,
,  ,
,
 . Пусть . Пусть  , ,  . Покажите, что . Покажите, что  - базис во множестве всех векторов плоскости параллелограмма. Найдите координаты векторов - базис во множестве всех векторов плоскости параллелограмма. Найдите координаты векторов 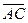 , ,  , , 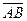 , ,  и и  . .
|  Рис. 8
Рис. 8
|
Решение. Так как векторы  неколлинеарны, то их можно взять за базисные в векторном пространстве всех векторов плоскости параллелограмма. Для нахождения координат любого вектора достаточно этот вектор выразить через базисные.
неколлинеарны, то их можно взять за базисные в векторном пространстве всех векторов плоскости параллелограмма. Для нахождения координат любого вектора достаточно этот вектор выразить через базисные.
Так как  , то
, то  . Так как
. Так как  , то
, то  . Так как
. Так как  , то
, то  . Так как
. Так как  , то
, то  . Так как
. Так как  , то
, то  .
.
Свойства координат (все свойства будем доказывать для трёхмерного векторного пространства).
10. В данном базисе каждый вектор имеет единственный набор координат.
Доказательство.
Пусть е =  - базис векторного пространства и
- базис векторного пространства и 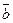 - любой вектор этого пространства. Предположим, что
- любой вектор этого пространства. Предположим, что 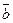 имеет два набора координат, т.е.
имеет два набора координат, т.е.  и
и  . Тогда
. Тогда 
 . Отсюда
. Отсюда  . Так как векторы
. Так как векторы  линейно независимы, то последнее равенство возможно только при нулевых коэффициентах. Следовательно, х1 = х2 , у1 = у2 , z1 = z2 .
линейно независимы, то последнее равенство возможно только при нулевых коэффициентах. Следовательно, х1 = х2 , у1 = у2 , z1 = z2 .
20. Если векторы заданы координатами в одном и том же базисе, то
а) при сложении (вычитании) векторов их соответствующие координаты складываются (вычитаются);
б) при умножении вектора на действительное число на это число умножается каждая его координата.
Доказательство.
Пусть е =  - базис векторного пространства,
- базис векторного пространства, 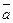 = {х1 , у1 , z1}и
= {х1 , у1 , z1}и 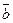 = {х2 , у2 , z2}. Тогда
= {х2 , у2 , z2}. Тогда  . Отсюда
. Отсюда  . Так как
. Так как  , то
, то  .
.
30. Два вектора коллинеарны тогда и только тогда, когда их координаты в одном и том же базисе пропорциональны. (Докажите самостоятельно.)
40. Три вектора компланарны тогда и только тогда, когда определитель, строчками которого являются координаты данных векторов, равен нулю. (Докажите самостоятельно.)
Задача 6. При каких значениях a и b векторы 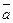 = {1, -2, a},
= {1, -2, a}, 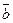 = {3, 1, 4} и
= {3, 1, 4} и  = {b, 0, 5} будут компланарными?
= {b, 0, 5} будут компланарными?
Решение. Векторы 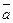 ,
, 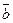 и
и  будут компланарными тогда и только тогда, когда будет равен нулю определитель из их координат, т.е.
будут компланарными тогда и только тогда, когда будет равен нулю определитель из их координат, т.е.  . Раскрыв определитель, получим 5 - 8b - ab + 30 = 0. Отсюда b (8 + a) = 35. При всех a и b, удовлетворяющих полученному условию, векторы будут компланарными, например, при a = -1 и b = 5.
. Раскрыв определитель, получим 5 - 8b - ab + 30 = 0. Отсюда b (8 + a) = 35. При всех a и b, удовлетворяющих полученному условию, векторы будут компланарными, например, при a = -1 и b = 5.