Основные действия над комплексными числами в алгебраической форме.
· Сложение комплексных чисел.Суммой двух комплексных чисел z1=а1+ib1 и z2=а2+ib2, называется комплексное число, определяемое равенством:
z1+z2=(а1+ib1)+(а2+ib2)=(а1+а2)+i(b1+b2).
· Вычитание комплексных чисел.Разностью двух комплексных чисел z1=а1+ib1 и z2=а2+ib2, называется такое комплексное число, которое, будучи сложено с z2, дает в сумме комплексное число z1:
z1-z2=(а1+ib1)-(а2+ib2)=(а1-а2)+i(b1-b2).
· Умножение комплексных чисел.Произведением комплексных чисел z1=а1+ib1 и z2=а2+ib2 называется такое комплексное число, которое получается, если мы перемножаем эти числа как двучлены по правилам алгебры, учитывая только, что: i2=-1, i3=(i2)·i=(-1)·i=-i, i4=(i2)2=(-i)·i=-i2=1, i5=i и т. д.,
z1 z2=(а1+ib1)(а2+ib2)=а1а2+ib1а2+iа1b2+i2b1b2;
z1 z2=(а1а2-b1b2)+i(а2b1+a1b2);
Замечание 1: Произведение сопряженных комплексных чисел z=а+ib и`z=а-ib есть действительное число и выражается так: z`z=а2+b2. Произведение сопряженных комплексных чисел равняется квадрату модуля каждого из них.
· Деление комплексных чисел.Деление комплексных чисел определяется как действие, обратное умножению.
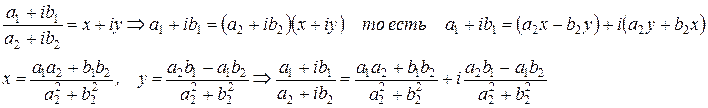
Замечание 2: Из правил действий над комплексными числами следует, что в результате операций сложения, вычитания, умножения и деления комплексных чисел получается снова комплексное число – замкнутость операций.
Если правила действий над комплексными числами применить к действительным числам, рассматривая их как частный случай комплексных, то эти правила будут совпадать с обычными правилами действий, известными из арифметики.
Замечание 3 Вернувшись к определениям суммы, разности, произведения и частного комплексных чисел, легко проверить, что если в этих выражениях заменить каждое комплексное число сопряженным, то и результаты указанных действий заменяются сопряженными числами.
Из замечания 3, в частности, вытекает следующая теорема:
Теорема:Если в многочлен А0хn+А1хn-1+...+Ап с действительными коэффициентами подставить вместо х число а+ib, а затем сопряженное число а-ib, то и результаты этих подстановок будут взаимно сопряженными.