Вопросы 1 и 2. Понятие комплексного числа. Арифметические операции над комплексными числами. Комплексная плоскость.

Лекция 1. Комплексные числа.

1. Понятие комплексного числа.

2. Арифметические операции над комплексными числами в алгебраической форме.

3. Комплексная плоскость.

4. Тригонометрическая и показательная форма комплексного числа.

 

 

Комплексные числа возникают в связи с задачей решения квадратных уравнений. Так, оставаясь в множестве действительных чисел, невозможно решить квадратное уравнение, дискриминант которого меньше нуля.

Комплексные числа необходимы в различных приложениях математики. В частности, теория функций комплексной переменной является действенным инструментом при использовании математических методов в различных областях науки.

 

 

 

 

 

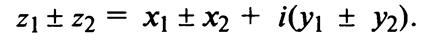
Нетрудно убедиться в том, что все арифметические операции над комплексными числами определяются естественным образом из правил сложения и умножения многочленов 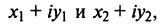если считать Например, произведение комплексных чисел есть

 

Пример 1. Даны комплексные числа: