Теорема о существовании единственности решения дифференциального уравнения 1 порядка
Дано дифференциальное уравнение 1 порядка  и функция f(x;y) непрерывна вместе с частными производными в некоторой области D плоскости XOY, тогда через точку М0(х0;y0)
и функция f(x;y) непрерывна вместе с частными производными в некоторой области D плоскости XOY, тогда через точку М0(х0;y0)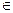 D проходит единственная кривая соответствующая частному решению дифференциального уравнения соответствующему начальному условию y(x0)=y0
D проходит единственная кривая соответствующая частному решению дифференциального уравнения соответствующему начальному условию y(x0)=y0
Через точку плоскости с данными координатами проходит 1 интегральная кривая.
Если не удаётся получить общее решение дифференциального уравнения 1 порядка в явном виде, т.е 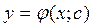 , то его можно получить в неявном виде:
, то его можно получить в неявном виде:
F(x; y; c) =0 – неявный вид
Общее решение в таком виде называется общим интегралом дифференциального уравнения.
По отношению к дифференциальному уравнению 1 порядка ставится 2 задачи:
1)Найти общее решение (общий интеграл)
2)Найти частное решение (частный интеграл) удовлетворяющее заданному начальному условию. Эту задачу называют задачей Коши для дифференциального уравнения.
Дифференциальные уравнения с разделяющимися переменными
Уравнения вида:  называется дифференциальным уравнением с разделяющимися переменными.
называется дифференциальным уравнением с разделяющимися переменными.
Подставим 

умножим на dx
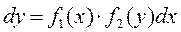
разделим переменные
разделим на 
Замечание: обязательно нужно рассматривать частный случай, когда 
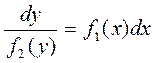
переменные разделены
проинтегрируем обе части уравнения
 - общее решение
- общее решение
Дифференциальное уравнение с разделяющимися переменными можно записать в виде:



Отдельный случай  !
!
Проинтегрируем обе части уравнения:
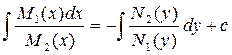
Примеры:
1)
2) нач. условия:
нач. условия: 