Глобал минимум туралы негізгі теорема

Келесі теорема тиімділіктің қажетті және жеткілікті шарттарын орнатады. Кез келген үшін функциясын үзіліссіз және бірінші, екінші ретті үзіліссіз дербес туындылары бар деп ұйғаралық. Онда келесі теорема дұрыс болады.

Теорема. нүктесі функциясының минимумы (локальды немесе глобальды) болуы үшін:

а) (стационарлық шарты);

б) гессиан , жартылай анықталған матрицаның оң болуы қажетті және жеткілікті болып табылады.

Бір айнымалылы функцияны минимумдау әдістері

 

Мақсатты функцияның унимодальды екені белгілі болып немесе анықталған интервалда мақсатты функцияның бір экстремумы бар және ол бізді қызықтыратын болса, онда полиномиальды аппроксимациялау әдісін қолдану қолайлы болады. Сонымен бұл әдістің идеясы төмендей.

Алдымен экстремум интервалдардың шекараларын орнатамыз. Ары қарай алынған интервалындағы нүктенің мақсатты функциясын өлшейміз. Сосын полиномды аппроксимацияланада мақсатты функция (әдетте, квадрат немесе куб көпмүшелік қарастырылады) көрсетілген нүктеден өтеді. Кейін аппроксимацияланаған көпмүшелік экстремумы табылады.

 

Кесіндіні қақ бөлу әдісі

Келесі әдістер тобы: дихотомия, Фибоначчи сандарын қолдану және алын қима әдістері.

Алдымен экстремум бар алғашқы интервалдарды бөлу, экстремумы жоқ ішкі интервалдарды сыртқы интервалдан шығарып тастау отыру қажет. Дихотомия әдісін қарастыралық. Бұл әдіс оптимумы бар интервал ұзындығын әр қадамда екі есе кішірейтуге мүмкіндік береді. Егер q функциясына n есептеу жүргізілген болса, онда интервал ұзындығын рет азайтуға мүмкіндік бар. Мейлі экстремум интервалынан табылсын. интервалын бөлейік. Ортасын деп аламыз, сосын екі нүктесінің арасынан , , бес нүктені аламыз. Унимодальдықты ескеріп, әруақытта интервалдар ішінен төртеудің екеуін алып тастау мүмкін (оптимум нүктесі егер табылмаса) және тек екі іргелес ішкі интервалдар және қалады.

Демек, барлығы жартылай ұзындықтағы (кесінді) есебіне келтіріледі.

 

25, 26 – ші дәрістер. ОЗ сызықтық моделдерінің мысалдары

Қорларды пайдалану есебі. Зауаттың m түрлі қорлары бар. і-ші қордың мөлшері в_і бірлікке тең . Бұл қорлардан n түрлі өнім шығарылады. Өндіріс j-ші өнімнің d_j бірлігінен көп шығарылмайды. J-ші өнімнің бірлігін шығару үшін і-ші қордың a_ij,бірлігі қажет. J-ші өнімнің бірлігін сатудан түсетін пайда C_j бірлік болды. Өндірісті шикізат қорын тиімді пайдаланып, өнімді сатудан түсетін жиын пайда ең үлкен мән қабылдайтындай етіп ұйымдастыру керек.

Егер айнымалы арқылы j-ші өнім мөлшерін белгілесек, онда қойылған есептің математикалық моделі келесі болады:

 

(1)

Емдәм құру есебі. Күндізгі емдәм құрамында m әр түрлі нәрлі зат болу керек. Әр түрлі заттың мөлшері b_i бірліктен кем емес болуы қажет. Мөлшерлері d_j n түрлі азық – түлік бар. a_ij-j-ші түрдегі азық-түлік құрамындағы і-ші түрлі нәрлі зат мөлшері, C_j-j-ші түрлі азық-түлік құны, х_j – жұмсалатын азық-түлік көлемі болсын. Онда математикалық тілде есеп былай жазылады:

(2)

 

Сызықты программалау есептерін шешу әдістері хақында.

Математикалық программалаудың бір бөлімі –сызықтық програмалаудың мәнін жақсы түсіну үшін таңертеңгі киінудің әзіл есебін қарастырайық.

Күнде таңертең оқуға немесе жұмысқа бару үшін адам киінеді. Мысалы, әр адам алты түрлі киім киеді деп есептейік: шұлық, бәтеңке, шалбар, костюм, жейде және галстук. Оның мақсаты –киінуге өте аз уақыт жұмсау. Киінудің көптеген варианттары бар, яғни киімдердің киілу реті әр түрлі болуы мүмкін. Бұл жағдайда киіну варианты 6 санының орны алмастыруына тең, яғни 6!=720.

Киіну вариантының жиынын шартты түрде 2 қосалқы жиынға бөлуге болады.

Біріншісі, мүмкін варианттар (мысалы, төмендегідей киіну мүмкін: шұлық, жейде, шалбар, галстук, бәтеңке, костюм), екіншісі –мүмкін емес варианттар (мысалы, бәтеңкеден кейін шұлық, галстуктен кейін жейде). Соынмен, мүмкін варианттарды таңдап алатындай шектеулер қойылуы мүмкін. Сонда мүмкін варианттардың ішінен ең аз уақытта іске асатынын таңдап алуға болады және ол ең тиімді немесе оптималды вариант болып табылады.

Бұл есеп математикалық программалау есептері типтес, себебі көптеген мүмкін шешімдері бар. Оның мақсаты мен шектеулерін қоса есептегендегі құрылымы математикалық программалау есептерінің құрылымына сәйкес келеді.

Математикалық программалауға сызықтықпен қатар құрамдас бөлігі ретінде бүтінсанды, параметрлік, сызықтық емес, квадратттық, схоластикалық, динамикалық программалау енеді.

Сызықтық программалау есептерінің ерекшеліктері сол, онда есептің мақсаты мен шектеулері, сызықтық функция түрінде беріледі.

Берілген сызықтық шектеулерді қанағаттандыратын сызықтық функцияның экстремумын (максимум және минимум) есептеп табу, сызықтық программалу есептері болып табылады.

Сызықтық программалаудың дамуы экономикамен тығыз байланысты. Әрбір кәсіпорын үшін өндірістің түрлі вариантын жоспарлауға болады. Кейбір көрсеткіштердің шамасына сәйкес жоспардың бір варианты жақсы, екіншісі –нашар болуы мүмкін. Өндіріс жоспарының нақты көрсеткіштерге сәйкес барынша тиімді болуы, ең көп пайда алуы, еңбек өнімділігінің жоғары болуы, т.с.с. жоспардың оптималды екендігін көрсетеді ал оны құру процесі оптималды жоспарлау деп аталады.

return false">ссылка скрыта

Сызықтық программалаудың негізін 1930 жылдары совет математигі Л.В.канторович қалады. Екінші дүнежүзілік соғыс жылдарында АҚШ қарулы күштерінің қызметін жоспарлау және қамтамасыз ету үшін сызықтық программалауды енгізді. 1941 ж. АҚШ-та сызықтық программалаудың ең негізгі есептерінің бірі көлік есебінің моделі жасалды.

Ал 1947 ж. американ ғалымы Дж. Данциг сызықтық программалау есептерін шешетін симплекс әдісін ойлап тапты.

1949 ж. Л:В. Канторович пен М.К. Гавурин көлік есебін шешетін тамаша әдіс-потенциал әдісін ұсынды. Кейінгі жылдары көптеген елдердің ғалымдары сызықтық программалаудың дамуына өз үлестерін қосты.

2.2. Экономикалық есептерді шығаруға арналған оптималдандыру модельдерін құру.

Экономикалық-математикалық модельдерді құру процесін шартты түрде төмендегідей негізгі кезеңдерге бөлуге болады.

Бірінші кезең –зерттеу объектісін таңдау. Зерттеу объектілеріне әр түрлі өндірістік-экономикалық процестер: жүк тасымалдау, өндірісті орналастыру, өнеркәсіп материалдарын іріктеу, т.с.с. жатады.

Екінші кезең –зерттеу мақсатын анықтау.

Ол берілген объектіні зерттеу кезіндегі есептің дұрыс қойылуына байланысты. Мысалы жүк тасымалын жоспарлаған кезде мынадай мақсат қоюға болады: транспорт шығынының минималды болуын қамтамасыз ететін жүк тасымалының жоспарын табу.

Үшінші кезең –оптималдылықтың критерийін таңдау. Оптималдылықтың критерийіне: жүк тасымалдаудың ең аз бағасы, максималды табыс, материалдардың ең төменгі бағасы, ең аз өндіріс шығындары, т.с.с. жатады. Критерийді таңдап алу кезінде өте ұқыпты болу қажет, себебі дұрыс таңдалмаған критерий қойылған есептің мақсатына сәйкес келмеуі ықтимал.

Төртінші кезең –негізгі шектеулерді анықтау.

Модельді құрған кезде негізгі шектеулерді анықтап, оларды модельге енгізу қажет. Нақты есептерде шектеулер өте көп болады. Енгізілетін шектердің мағынасы да әр түрлі. Әрбір экономикалық есеп ресурс бойынша шектелген: шикізат, материал, машина, құрал-жабдықтар, жұмысшы күші т.б. Есепке ресурстардан басқа қосымша шектер қойылады. Мысалы өнім ассортиментін, сапасын, сұранымды қанағаттандыруын, өндіру уақытын есепке алу қажет. Дұрыс шешім алу үшін шектеулер теңдеулер мен теңсіздіктер системалары түрінде беріледі. Қарапайым екі түрлі экономикалық есептің моделін құрып, олардың сызықтық программалау есептеріне жататындығын көрсетейік.

Кәсіпорынға мөлшерлері шектеулі үш түрлі шикізатының екі түрлі өнім түрлерін дайындау қажет. Алғашқы мәліметтер төмендегі кестеде келтірілген: Кесте 2.1.

Шикізат түрлері	Шикізат қорлары	Өнім бірлігін өндіруге жұмсалатын шикізат мөлшері
Өнім бірлігінен алынатын пайда

Өндірілген өнімді өткізгенде ең көп пайда алынатын өнім шығару жоспарын құру қажет.

Модель құруды белгісіздер енгізуден бастаймыз. деп
өнімінің өндірілетін санын, деп өнімінің өндірілетін санын белгілейміз.

Қарастырып отырған есепке зерттеу объектісіне шектеулі шикізат қорын пайдалана отырып, өнім өндіруді жоспарлау жатады.

Зерттеудің мақсатына –максимал табыс әкелетін өнім өндірудің жоспарын құру жатады.есептің критерийі –максималды табыс. Осы критерийді формула түрінде жазайық.

Өнімінің бір өлшемін өткізгенде 12 тг пайда аламыз, оның жалпы саны – , ал барлық өнімінен алынатын пайда 12 тг.

өнімінің бір өлшемін өткізгенде 15 тг пайда, оның жалпы саны - . Барлық -өнімі өткізілгендегі табыс -15 тг.

және өнімін өткізгендегі пайда максималды болуы қажет, сонда есептің критерийі

Кәсіпорындағы шикізат қорының шектеулілігі белгілі. Ол да модельде көрсетілуі қажет. Кәсіпорын үш түрлі шикізат қолданады. Әрбір шикізаттан жұмсалған қор шығыны сол шикізаттардың қорларынан аспауы қажет және ол төмендегідей жазылады.

Кәсіпорын шығаратын өнімнің мөлшері оң шама немесе 0-ге тең болады. Сондықтан модельге айнымалылардың теріс еместік шарты қатысуы қажет.

Сонымен құрылған өрнектерді жинақтап, шикізатты пайдалану есебінің математикалық моделін аламыз.

(2.1)

Бұл есептің ерекшелігі мынадай: берілген шектеулерді қанағаттандыратын және өнімдерінің мөлшері, яғни мен орынға максимал пайда әкелетін өнім шығаратын вариантты таңдап алу қажет. Ол вариант оптималды деп аталады. -мақсат функциясы және есептің шектеулері сызықтық йункция болады.

Қорды пайдалану есептері сызықтық программалау есептеріне жатады және әр түрлі қорларды пайдаланып өнім өндіретін кәсіпорындарда қолданылады.

Осы ерекшеліктерін ескере отырып, есептің жалпы түрінің моделін жазуға болады.

Кәсіпорын m түрлі пайдалана отырып, n түрлі өнім шығарсын дейік. Төмендегідей белгілеулер енгіземіз:

i-ші ресурс қоры;

-ші өнімнің бірлігін өндіруге жұмсалатын –ші ресурстың мөлшері;

-ші өнімнің бір өлшемінен түсетін пайда.

Сатылғаннан соң максималды пайда табатын өнім өндіру жоспарын құру керек.

-арқылы –j-ші мөлшерін белгілейміз.

Қорларды пайдалану есебінің жалпы математикалық моделін төмендегідейжазуға болады:

(2.2)

 

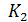Ірі қара малын бордақылау үшін екі түрлі және жемдерінен қоспа жасау керек. Қоспаның бір ірі қара малына арналған бөлігінде төмендегідей нәрлі заттар берілген: -12 бірліктен кем емес, 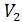-6 бірліктен кем емес, -9 бірліктен кем емес.

Қалған мәліметтер мына кестеде берілген: Кесте 2.2.

Нәрлі заттар	Жемнің бірлігіндегі нәрлі зат мөлшері
Жемнің бірлігінің бағасы:

Қоспаның құнарлығын сақтай отырып, минималды шығын жұмсалатын жем қоспасының мөлшерін табу керек.

Модель құруды белгісіздер енгізуден бастаймыз. деп жемінің мөлшерін, 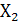деп жемінің мөлшерін белгілейміз.

Берілген есептің зерттеу объектісіне қоспаны жасау жатады. Қосылатын шикізаттардың мөлшері мен тағамдық заттардың (белок, май, көміртегі, т.с.с.) өлшем бірліктері әр түрлі болуы мүмкін, мысалы шикізаттар –т, кг, ал тағамдық заттар – г беріледі.

Зерттеу мақсаты –жемге аз шығын жұмсай отырып, қоспаның берілген жұғымдылығын қамтамасыз ету.

Есептің критерийі –минималды шығын.

Осы критерийді формула түрінде қарайық.

жемінің бағасы 2 теңге, ал мөлшері - , ал барлық 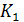жемінің бағасы 2 теңге болады. жемінің бағасы 3 теңге де мөлшері - , сондықтан барлық жемінің бағасы 3 теңге.

Екінші жағынан және қоспасының бағасы минималды болатындықтан, есептің критерийін төмендегідей жазуға болады:

Есептің берілгені бойынша қоспа үш түрлі нәрлі заттан тұрады және әрбір нәрлі зат берілген мөлшерден кем болмауы қажет, яғни қоспаның берілген жұғымдылығын (сапасын) қамтамасыз ету керек. Әрбір нәрлі заттың берілген мөлшерін пайдалана отырып, төмендегідей шектеулерді жазамыз:

Қоспадағы жемнің мөлшері оң сан немесе 0-ге тең (егер жемнің бір түрі жоқ болса). Сондықтан модельде айнымалылардың теріс еместік шарты көрсетілуі қажет:

Берілген қоспа есебінің моделін төмендегідей жазуға болады:

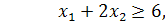
(2.3)

Берілген есептің ерекшелігі сол, 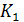және жемдерін қосудың бірнеше вариантын, яғни берілген шектеулерді қанағаттандыратын мен мәндерінің көптеп табуға болады. Бірақ бізге ең аз шығын жұмсалатын вариантын таңдап алу қажет. Сол вариант қоспаның оптималды варианты болып табылады. Сондықтан берілген есептің -мақсат функциясы мен шектеулері сызықтық болғандықтан сызықтық программалау есептеріне жатады.

Қоспаның қарастырылған жеке есебін жалпы түрге келтірейік. Жемнің түрі n, ал нәрлі заттың түрі m болсын. Қоспа бөлігінде і-ші нәрлі затының мөлшері -ден кем емес. 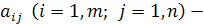i нәрлі затының j –жем бірлігіндегі мөлшері; жемінің бірлігінің бағасы.

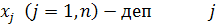-ші жем мөлшерін белгілейміз. Сонда қоспа есебінің жалпы түрі мынадай модельмен беріледі:

 

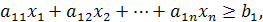
(2.4)

Қосынды белгісін пайдаланып отырып (2.4) есебін төмендегідей жазуға болады:

 

 

 

(i=1,m),

 

(j=1,n).

(2.2) және (2.4) есептерін матрица түрінде де жазуға болады. Белгілеулер енгізейік: 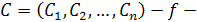функциясындағы белгісіздер коэффициенттері жол матрица;

 

 

А= - технологиялық матрица

 

B= 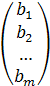-шектеулердің бос мүшелерінің матрица –бағанасы;

X= 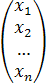-белгісіздердің матрица –бағанасы

 

Сонда (2.2) есебінің матрицалық формасы төмендегідей жазылады:

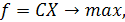
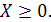(2.5)

Ал (2.4) есебінің түрі:

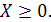
Сызықтық программалау есептерінде шектеулер теңдік түрін де де берілуі мүмкін, ал мақсат функциясы максимумға немесе минимумға шығарылады. Мұндай есептердің матрицалық формасы

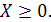(2.7)

(2.5), (2.6.), (2.7) есептері сызықтық программалаудың жеке түрлері болып табылады. Олардың ерекшеліктері шектеулері бір ғана түрлі. Осылармен қатар сызықтық программалау есептерінде аралас шектеулері бар ( есептер де көп тараған.

27, 28 – ші дәрістер. ОЗ бүтін санды сызықтық моделдерінің мысалдары: материалдарды пішу есебі, тағайындау туралы есеп, қоржын туралы есеп, коммивояжер есебі.

Бүтін санды есептер – шешімі бүтін сан болуды қажет ететін есептер.

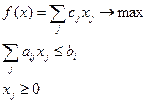
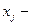бүтін сандар (бүтін сандылық шарты)

-нөльдік айнымалылар (бүтін санды есептерге жатады).