Тема 1.1 Характеристика электрического поля. Напряженность, потенциал (напряжения). Закон Кулона. Проводники и диэлектрики в электрическом поле.

РАЗДЕЛ 1 ЭЛЕКТРОТЕХНИКА. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА

Закон сохранения электрического заряда

Еще в глубокой древности было известно, что янтарь, потертый о шерсть, притягивает легкие предметы. Английский врач Джильберт (конец XVI в.) назвал тела, способные после натирания притягивать легкие предметы, наэлектризованными. Сейчас мы гово­рим, что тела при этом приобретают электрические заряды. Несмотря на огромное разнообразие веществ в природе, существует только два типа электрических зарядов: заряды, подобные возникающим на стекле, потертом о кожу (их назвали положитель­ными), и заряды, подобные возникающим на эбоните, потертом о мех (их назвали отрицательными), одноименные заряды друг от друга отталкиваются, разноимен­ные — притягиваются.

Опытным путем (1910—1914) американский физик Р. Милликен (1868—1953) пока­зал, что электрический заряддискретен, т. е. заряд любого тела составляет целое кратное отэлементарного электрического заряда е (е=1,6×10^–19 Кл). Электрон (m_e=9,11×10^–31 кг) ипротон (т_p= 1,67×10^–27 кг) являются соответственно носителями элементарных отрицательного и положительного зарядов.

Все тела в природе способны электризоваться, т. е. приобретать электрический заряд. Электризация тел может осуществляться различными способами: соприкоснове­нием (трением), электростатической индукцией и т. д. Всякий процесс заряжения сводится к разделению зарядов, при котором на одном из тел (или части тела) появляется избыток положительного заряда, а на другом (или другой части тела) — избыток отрицательного заряда. Общее количество зарядов обоих знаков, содержащихся в телах, не изменяется: эти заряды только перераспределяются между телами.

Из обобщения опытных данных был установлен фундаментальный закон природы, экспериментально подтвержденный в 1843 г. английским физиком М. Фарадеем (1791—1867), —закон сохранения заряда: алгебраическая сумма электрических зарядов любой замкнутой системы (системы, не обменивающейся зарядами с внешними тела­ми) остается неизменной, какие бы процессы ни происходили внутри этой системы.

Электрический заряд — величина релятивистски инвариантная, т. е. не зависит от системы отсчета, а значит, не зависит от того, движется этот заряд или покоится.

В зависимости от концентрации свободных зарядов тела делятся на проводники, диэлектрики и полупроводники.Проводники — тела, в которых электрический заряд может перемещаться по всему его объему. Проводники делятся на две группы: 1)про­водники первого рода (металлы) — перенос в них зарядов (свободных электронов) не сопровождается химическими превращениями; 2)проводники второго рода (например, расплавленные соли, растворы кислот) — перенос в них зарядов (положительных и отрицательных ионов) ведет к химическим изменениям. Диэлектрики (например, стекло, пластмассы) — тела, в которых практически отсутствуют свободные заряды. Полупроводники (например, германий, кремний) занимают промежуточное положение между проводниками и диэлектриками. Указанное деление тел является весьма усло­вным, однако большое различие в них концентраций свободных зарядов обусловливает огромные качественные различия в их поведении и оправдывает поэтому деление тел на проводники, диэлектрики и полупроводники.

Единица электрического заряда (производная единица, так как определяется через единицу силы тока) — кулон (Кл) — электрический заряд, проходящий через попереч­ное сечение проводника при силе тока 1 А за время 1 с.

Закон Кулона

Закон взаимодействия неподвижных точечных электрических зарядов установлен в 1785 г. Ш. Кулоном с помощью крутильных весов, подобных тем, которые использовались Г. Кавендишем для определения гравитационной постоянной (ранее этот закон был открыт Г. Кавендишем, однако его работа оставалась неизвестной более 100 лет). Точечным называется заряд, сосредоточенный на теле, линейные раз­меры которого пренебрежимо малы по сравнению с расстоянием до других заряжен­ных тел, с которыми он взаимодействует. Понятие точечного заряда, как и материаль­ной точки, является физической абстракцией.

Закон Кулона:сила взаимодействия F между двумя неподвижными точечными зарядами, находящимися в вакууме, пропорциональна зарядам Q₁ и Q₂ и обратно пропорциональна квадрату расстояния r между ними:

где k — коэффициент пропорциональности, зависящий от выбора системы единиц.

Сила F направлена по прямой, соединяющей взаимодействующие заряды, т. е. является центральной, и соответствует притяжению (F<0) в случае разноименных зарядов и отталкиванию (F>0) в случае одноименных зарядов. Эта сила называется кулоновской силой. В векторной форме закон Кулона имеет вид

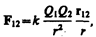(1.1)

где F₁₂ — сила, действующая на заряд Q₁ со стороны заряда Q₂, r₁₂ — радиус-вектор, соединяющий заряд Q₂ с зарядом Q₁, r = |r₁₂| (рис. 1). На заряд Q₂ со стороны заряда Q₁ действует сила F₂₁ = –F₁₂.

В СИ коэффициент пропорциональности равен

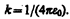
Тогда закон Кулона запишется в окончательном виде:

(1.2)

Величина e₀ называется электрической постоянной; она относится к числу фундамен­тальных физических постоянных и равна

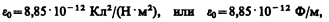(1.3)

гдефарад (Ф) — единица электрической емкости. Тогда

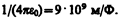
Электростатическое поле. Напряженность электростатического поля

Если в пространство, окружающее электрический заряд, внести другой заряд, то на него будет действовать кулоновская сила; значит, в пространстве, окружающем элект­рические заряды, существует силовое поле. Согласно представлениям современной физики, поле реально существует и наряду с веществом является одной из форм существования материи, посредством которого осуществляются определенные взаимо­действия между макроскопическими телами или частицами, входящими в состав вещества. В данном случае говорят об электрическом поле — поле, посредством которого взаимодействуют электрические заряды. Мы будем рассматривать элект­рические поля, которые создаются неподвижными электрическими зарядами и называ­ются электростатическими.

Для обнаружения и опытного исследования электростатического поля используется пробный точечный положительный заряд — такой заряд, который не искажает исследу­емое поле (не вызывает перераспределения зарядов, создающих поле). Если в поле, создаваемое зарядом Q, поместить пробный заряд Q₀, то на него действует сила F, различная в разных точках поля, которая, согласно закону Кулона (78.2), пропорци­ональна пробному заряду Q₀. Поэтому отношение F/Q₀ не зависит от Q₀ и характеризу­ет электростатическое поле в той точке, где пробный заряд находится. Эта величина называется напряженностью и является силовой характеристикой электростатичес­кого поля.

Напряженность электростатического поля в данной точке есть физическая величина, определяемая силой, действующей на пробный единичный положительный заряд, помещенный в эту точку поля:

(1.4)

Как следует из формул (1.4) и (1.1), напряженность поля точечного заряда в вакууме

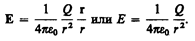(1.5)

Направление вектора Е совпадает с направлением силы, действующей на положитель­ный заряд. Если поле создается положительным зарядом, то вектор Е направлен вдоль радиуса-вектора от заряда во внешнее пространство (отталкивание пробного положи­тельного заряда); если поле создается отрицательным зарядом, то вектор Е направлен к заряду (рис. 2).

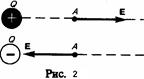
Из формулы (1.4) следует, что единица напряженности электростатического по­ля — ньютон на кулон (Н/Кл): 1 Н/Кл — напряженность такого поля, которое на точечный заряд 1 Кл действует с силой в 1 Н; 1 Н/Кл= 1 В/м, где В (вольт) — еди­ница потенциала электростатического поля .

Графически электростатическое поле изображают с помощьюлиний напряженности — линий, касательные к которым в каждой точке совпадают с направлением вектора Е (рис. 3). Линиям напряженности приписывается направление, совпадающее с направлением вектора напряженности. Так как в каждой данной точке пространства вектор напряженности имеет лишь одно направление, то линии напряженности никогда не пересекаются. Дляоднородного поля (когда вектор напряженности в любой точке постоянен по величине и направлению) линии напряженности параллельны вектору напряженности. Если поле создается точечным зарядом, то линии напряженности — радиальные прямые, выходящие из заряда, если он положителен (рис. 4, а), и входя­щие в него, если заряд отрицателен (рис. 4, б). Вследствие большой наглядности графический способ представления электростатического поля широко применяется в электротехнике.

Чтобы с помощью линий напряженности можно было характеризовать не только направление, но и значение напряженности электростатического поля, условились про­водить их с определенной густотой (см. рис. 3): число линий напряженности, прони­зывающих единицу площади поверхности, перпендикулярную линиям напряженности, должно быть равно модулю вектора Е. Тогда число линий напряженности, пронизыва­ющих элементарную площадку dS, нормаль n которой образует угол a с вектором Е, равно Е dS cosa = E_ndS, где Е_п—проекция вектора Е на нормаль n к площадке dS. Величина

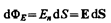
называетсяпотоком вектора напряженности через площадку dS. Здесь dS = dSn — век­тор, модуль которого равен dS, а направление совпадает с направлением нормали n к площадке. Выбор направления вектора n (а следовательно, и dS) условен, так как его можно направить в любую сторону. Единица потока вектора напряженности электростатического поля — 1 В×м.

Для произвольной замкнутой поверхности S поток вектора Е сквозь эту поверх­ность

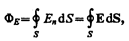(1.6)

где интеграл берется по замкнутой поверхности S. Поток вектора Е является алгебра­ической величиной: зависит не только от конфигурации поля Е, но и от выбора направления n. Для замкнутых поверхностей за положительное направление нормали принимается внешняя нормаль, т. е. нормаль, направленная наружу области, охватыва­емой поверхностью.

Потенциал электростатического поля

Тело, находящееся в потенциальном поле сил (а электростатическое поле является потенциальным), обладает потенциальной энергией, за счет которой силами поля совершается работа. Как известно, работа консервативных сил совершается за счет убыли потенциальной энергии. Поэтому работу сил электро­статического поля можно представить как разность потенциальных энергий, которыми обладает точечный заряд Q₀ в начальной и конечной точках поля заряда Q:

(1.7)

откуда следует, что потенциальная энергия заряда qq в поле заряда Q равна

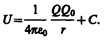
Она, как и в механике, определяется неоднозначно, а с точностью до произвольной постоянной С. Если считать, что при удалении заряда в бесконечность (r®¥) потенци­альная энергия обращается в нуль (U=0), то С=0 и потенциальная энергия заряда Q₀, находящегося в поле заряда Q на расстоянии г от него, равна

(1.8)

Для одноименных зарядов Q₀Q>0 и потенциальная энергия их взаимодействия (оттал­кивания) положительна, для разноименных зарядов Q₀Q<0 и потенциальная энергия их взаимодействия (притяжения) отрицательна.

Если поле создается системой n точечных зарядов Q₁, Q₂, ..., Q_n, то работа электростатических сил, совершаемая над зарядом Q₀, равна алгебраической сумме работ сил, обусловленных каждым из зарядов в отдельности. Поэтому потенциальная энергия U заряда Q₀, находящегося в этом поле, равна сумме потенциальных энергий U_i, каждого из зарядов:

(1.9)

Из формул (1.8) и (1.9) вытекает, что отношение U/Q₀ не зависит от Q₀ и является поэтому энергетической характеристикой электростатического поля, называемой по­тенциалом:

(1.10)

Потенциал j в какой-либо точке электростатического поля есть физическая величина, определяемая потенциальной энергией единичного положительного заряда, помещен­ного в эту точку.

Следовательно, потенциал поля, создаваемого точечным зарядом Q, равен

(1.11)

Работа, совершаемая селами электростатического поля при перемещении заряда Q₀ из точки 1 в точку 2 , может быть представлена как

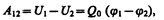(1.12)

т. е. равна произведению перемещаемого заряда на разность потенциалов в начальной и конечной точках.Разность потенциалов двух точек 1 и 2 в электростатическом поле определяется работой, совершаемой силами поля, при перемещении единичного поло­жительного заряда из точки 1 в точку 2.

Работа сил поля при перемещении заряда Q₀ из точки 1 в точку 2 может быть записана также в виде

(1.13)

Приравняв (1.12) и (1.13), придем к выражению для разности потенциалов:

(1.14)

где интегрирование можно производить вдоль любой линии, соединяющей начальную и конечную точки, так как работа сил электростатического поля не зависит от траек­тории перемещения.

Если перемещать заряд Q₀ из произвольной точки за пределы поля, т. е. в бесконеч­ность, где, по условию, потенциал равен нулю, то работа сил электростатического поля, согласно (1.11), A_¥=Q₀j, откуда

(1.5)

Таким образом, потенциал — физическая величина, определяемая работой по переме­щению единичного положительного заряда при удалении его из данной точки поля в бесконечность. Эта работа численно равна работе, совершаемой внешними силами (против сил электростатического поля) по перемещению единичного положительного заряда из бесконечности в данную точку поля.

Из выражения (1.10) следует, что единица потенциала —вольт (В): 1 В есть потен­циал такой точки поля, в которой заряд в 1 Кл обладает потенциальной энергией 1 Дж (1 В = 1 Дж/Кл). Учитывая размерность вольта, можно показать, что введенная единица напряженности электростатического поля действительно равна 1 В/м: 1 Н/Кл=1 Н×м/(Кл×м)=1 Дж/(Кл×м)=1 В/м.

Из формул (1.9) и (1.10) вытекает, что если поле создается несколькими зарядами, то потенциал поля системы зарядов равен алгебраической сумме потенциалов полей всех этих зарядов:

Для графического изображения распределения потенциала электростатического поля,как и в случае поля тяготения, пользуютсяэквипотенциальными поверхностями — поверхностями, во всех точках которых потенциал j имеет одно и то же значение.

Если поле создается точечным зарядом, то его потенциал, 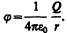Таким образом, эквипотенциальные поверхности в данном случае — кон­центрические сферы. С другой стороны, линии напряженности в случае точечного заряда — радиальные прямые. Следовательно, линии напряженности в случае точеч­ного заряда перпендикулярны эквипотенциальным поверхностям.

Линии напряженности всегда нормальны к эквипотенциальным поверхностям. Дей­ствительно, все точки эквипотенциальной поверхности имеют одинаковый потенциал, поэтому работа по перемещению заряда вдоль этой поверхности равна нулю, т. е. электростатические силы, действующие на заряд, всегда направлены по нормалям к эквипотенциальным поверхностям. Следовательно, вектор Е всегда нормален к эк­випотенциальным поверхностям, а поэтому линии вектора Е ортогональны этим повер­хностям.

Эквипотенциальных поверхностей вокруг каждого заряда и каждой системы заря­дов можно провести бесчисленное множество. Однако их обычно проводят так, чтобы разности потенциалов между любыми двумя соседними эквипотенциальными поверх­ностями были одинаковы. Тогда густота эквипотенциальных поверхностей наглядно характеризует напряженность поля в разных точках. Там, где эти поверхности рас­положены гуще, напряженность поля больше.

Итак, зная расположение линий напряженности электростатического поля, можно построить эквипотенциальные поверхности и, наоборот, по известному расположению эквипотенциальных поверхностей можно определить в каждой точке поля модуль и направление напряженности поля. На рис. 133 для примера показан вид линий напряженности (штриховые линии) и эквипотенциальных поверхностей (сплошные линии) полей положительного точечного заряда (а) и заряженного металлического цилиндра, имеющего на одном конце выступ, а на другом — впадину (б)

Принцип суперпозиции электростатических полей.

Рассмотрим метод определения модуля и направления вектора напряженности Е в каждой точке электростатического поля, создаваемого системой неподвижных зарядов Q₁, Q₂, ..., Q_n.

Опыт показывает, что к кулоновским силам применим рассмотренный в механике принцип независимости действия сил, т. е. результирующая сила F, дейст­вующая со стороны поля на пробный заряд Q₀, равна векторной сумме сил F_i, приложенных к нему со стороны каждого из зарядов Q_i:

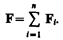(80.1)

F= Q₀E и F_i = Q₀Е_i, где Е—напряженность результирующего поля, а Е_i — напряженность поля, создаваемого зарядом Q_i. Подставляя последние выраже­ния в (80.1), получаем

(80.2)

Формула (80.2) выражаетпринцип суперпозиции (наложения) электростатических полей, согласно которому напряженность Е результирующего поля, создаваемого системой зарядов, равна геометрической сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности.

Принцип суперпозиции позволяет рассчитать электростатические поля любой си­стемы неподвижных зарядов, поскольку если заряды не точечные, то их можно всегда свести к совокупности точечных зарядов.

Проводники в электростатическом поле

Если поместить проводник во внешнее электростатическое поле или его зарядить, то на заряды проводника будет действовать электростатическое поле, в результате чего они начнут перемещаться. Перемещение зарядов (ток) продолжается до тех пор, пока не установится равновесное распределение зарядов, при котором электростатическое поле внутри проводника обращается в нуль. Это происходит в течение очень короткого времени. В самом деле, если бы поле не было равно нулю, то в проводнике возникло бы упорядоченное движение зарядов без затраты энергии от внешнего источника, что противоречит закону сохранения энергии. Итак, напряженность поля во всех точках внутри проводника равна нулю:

Е = 0

Отсутствие поля внутри проводника означает, согласно (85.2), что потенциал во всех точках внутри проводника постоянен (j = const), т. е. поверхность проводника в электростатическом поле является эквипотенциальной.

Отсюда же следует, что вектор напряженности поля на внешней поверхности проводника направлен по нормали к каждой точке его поверхности. Если бы это было не так, то под действием касательной составляющей Е заряды начали бы по поверхности проводника переме­щаться, что, в свою очередь, противоречило бы равновесному распределению зарядов(Рис.141).

Если проводнику сообщить некоторый заряд Q, то нескомпенсированные заряды располагаются только на поверхности проводника.

Если во внешнее электростатическое поле внести нейтральный проводник, то свободные заряды (электроны, ионы) будут перемещаться: положительные — по полю, отрицательные — против поля (рис. 142, а). На одном конце проводника будет скап­ливаться избыток положительного заряда, на другом — избыток отрицательного. Эти заряды называютсяиндуцированными. Процесс будет происходить до тех пор, пока напряженность поля внутри проводника не станет равной нулю, а линии напряжен­ности вне проводника — перпендикулярными его поверхности (рис. 142, б). Таким образом, нейтральный проводник, внесенный в электростатическое поле, разрывает часть линий напряженности; они заканчиваются на отрицательных индуцированных зарядах и вновь начинаются на положительных. Индуцированные заряды распределяются на внешней поверхности проводника. Явление перераспределения поверхностных зарядов на проводнике во внешнем электростатическом поле называется электростати­ческой индукцией.

Таккак в состоянии равновесия внутри проводника заряды отсутствуют, то созда­ние внутри него полости не повлияет на конфигурацию расположения зарядов и тем самым на электростатическое поле. Следовательно, внутри полости поле будет отсут­ствовать. Если теперь этот проводник с полостью заземлить, то потенциал во всех точках полости будет нулевым, т. е. полость полностью изолирована от влияния внешних электростатических полей. На этом основанаэлектростатическая защи­та — экранирование тел, например измерительных приборов, от влияния внешних электростатических полей. Вместо сплошного проводника для защиты может быть использована густая металлическая сетка, которая, кстати, является эффективной при наличии не только постоянных, но и переменных электрических полей.

Типы диэлектриков. Поляризация диэлектриков

Диэлектрик (как и всякое вещество) состоит из атомов и молекул. Так как положитель­ный заряд всех ядер молекулы равен суммарному заряду электронов, то молекула в целом электрически нейтральна. Если заменить положительные заряды ядер молекул суммарным зарядом + Q, находящимся в центре «тяжести» положительных зарядов, а заряд всех электронов — суммарным отрицательным зарядом – Q, находящимся в центре «тяжести» отрицательных зарядов, то молекулу можно рассматривать как электрический диполь с электрическим моментом, определяемым формулой (80.3).

Первую группу диэлектриков (N₂, Н₂, О₂, СО₂, СН₄, ...) составляют вещества, молекулы которых имеют симметричное строение, т. е. центры «тяжести» положитель­ных и отрицательных зарядов в отсутствие внешнего электрического поля совпадают и, следовательно, дипольный момент молекулы р равен нулю.Молекулы таких диэлект­риков называютсянеполярными. Под действием внешнего электрического поля заряды неполярных молекул смещаются в противоположные стороны (положительные по полю, отрицательные против поля) и молекула приобретает дипольный момент.

Вторую группу диэлектриков (H₂O, NН₃, SO₂, CO,...) составляют вещества, молеку­лы которых имеют асимметричное строение, т. е. центры «тяжести» положительных и отрицательных зарядов не совпадают. Таким образом, эти молекулы в отсутствие внешнего электрического поля обладают дипольным моментом.Молекулы таких диэлектриков называютсяполярными. При отсутствии внешнего поля, однако, дипольные моменты полярных молекул вследствие теплового движения ориентированы в про­странстве хаотично и их результирующий момент равен нулю. Если такой диэлектрик поместить во внешнее поле, то силы этого поля будут стремиться повернуть диполи вдоль поля и возникает отличный от нуля результирующий момент.

Третью группу диэлектриков (NaCl, KCl, КВr, ...) составляют вещества, молекулы которых имеют ионное строение. Ионные кристаллы представляют собой простра­нственные решетки с правильным чередованием ионов разных знаков. В этих кри­сталлах нельзя выделить отдельные молекулы, а рассматривать их можно как систему двух вдвинутых одна в другую ионных подрешеток. При наложении на ионный кристалл электрического поля происходит некоторая деформация кристаллической решетки или относительное смещение подрешеток, приводящее к возни­кновению дипольных моментов.

Таким образом, внесение всех трех групп диэлектриков во внешнее электрическое поле приводит к возникновению отличного от нуля результирующего электрического момента диэлектрика, или, иными словами, к поляризации диэлектрика.Поляризациейдиэлектрика называется процесс ориентации диполей или появления под воздействием внешнего электрического поля ориентированных по полю диполей.

Соответственно трем группам диэлектриков различают три вида поляризации:

электронная, илидеформационная, поляризация диэлектрика с неполярными молеку­лами, заключающаяся в возникновении у атомов индуцированного дипольного момен­та за счет деформации электронных орбит;

ориентационная, илидипольная, поляризация диэлектрика с полярными молекулами, заключающаяся в ориентации имеющихся дипольных моментов молекул по полю. Естественно, что тепловое движение препятствует полной ориентации молекул, но в результате совместного действия обоих факторов (электрическое поле и тепловое движение) возникает преимущественная ориентация дипольных моментов молекул по полю. Эта ориентация тем сильнее, чем больше напряженность электрического поля и ниже температура;

ионная поляризация диэлектриков с ионными кристаллическими решетками, заклю­чающаяся в смещении подрешетки положительных ионов вдоль поля, а отрицатель­ных — против поля, приводящем к возникновению дипольных моментов.

Поляризованность. Напряженность поля в диэлектрике

При помещении диэлектрика во внешнее электрическое поле он поляризуется, т. е. приобретает отличный от нуля дипольный момент гдер_i — дипольный момент одной молекулы. Для количественного описания поляризации диэлектрика пользуются векторной величиной —поляризованностью, определяемой как дипольный момент единицы объема диэлектрика:

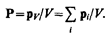(88.1)

Из опыта следует, что для большого класса диэлектриков (за исключением сегнетоэлектриков, поляризованность Р линейно зависит от напряженности поля Е. Если диэлектрик изотропный и Е не слишком велико, то

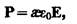(88.2)

где æ —диэлектрическая восприимчивость вещества, характеризующая свойства ди­электрика; æ – величина безразмерная; притом всегда æ > 0 и для большинства диэлек­триков (твердых и жидких) составляет несколько единиц (хотя, например, для спирта æ »25, для воды æ =80).

Для установления количественных закономерностей поля в диэлектрике внесем в однородное внешнее электрическое поле Е₀ (создается двумя бесконечными парал­лельными разноименно заряженными плоскостями) пластинку из однородного диэлек­трика, расположив ее так, как показано на рис. 135. Под действием поля диэлектрик поляризуется, т. е. происходит смещение зарядов: положительные смещаются по полю, отрицательные — против поля. В результате этого на правой грани диэлектрика, обращенного к отрицательной плоскости, будет избыток положительного заряда с поверхностной плотностью +s', на левой — отрицательного заряда с поверхностной плотностью –s'. Эти нескомпенсированные заряды, появляющиеся в результате поля­ризации диэлектрика, называютсясвязанными. Так как их поверхностная плотность s' меньше плотности s свободных зарядов плоскостей, то не все поле Е компенсируется полем зарядов диэлектрика: часть линий напряженности пройдет сквозь диэлектрик, другая же часть — обрывается на связанных зарядах. Следовательно, поляризация диэлектрика вызывает уменьшение в нем поля по сравнению с первоначальным внеш­ним полем. Вне диэлектрика Е=Е₀.

Таким образом, появление связанных зарядов приводит к возникновению допол­нительного электрического поля Е' (поля, создаваемого связанными зарядами), кото­рое направлено против внешнего поля Е₀ (поля, создаваемого свободными зарядами) и ослабляет его. Результирующее поле внутри диэлектрика

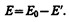
Поле Е'=s'/e₀ (поле, созданное двумя бесконечными заряженными плоскостями; см. формулу (82.2)), поэтому

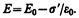(88.3)

Определим поверхностную плотность связанных зарядов s'. По (88.1), полный дипольный момент пластинки диэлектрика p_V =PV = PSd, где S — площадь грани пластинки, d — ее толщина. С другой стороны, полный дипольный момент, согласно (80.3), равен произведению связанного заряда каждой грани Q' =s' S на расстояние d между ними, т. е. р_V = s' Sd. Таким образом, PSd= s' Sd, или

(88.4)

т. е. поверхностная плотность связанных зарядов s' равна поляризованности Р. Подставив в (88.3) выражения (88.4) и (88.2), получим

откуда напряженность результирующего поля внутри диэлектрика равна

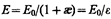(88.5)

 

 

Безразмерная величина

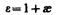(88.6)

называетсядиэлектрической проницаемостью среды. Сравнивая (88.5) и (88.6), видим, что e показывает, во сколько раз поле ослабляется диэлектриком, и характеризует количественно свойство диэлектрика поляризоваться в электрическом поле.

 

Литература:

1. Жаворонков М.А., Кузин А.В. Электротехника и электроника. Москва,

АСАДЕМ!А, 2005.

2. Касаткин А.С., Немцов М.В. Электротехника. Москва, Высшая школа, 2003

3. Петленко Б.И. Электротехника и электроника. Москва,

АСАДЕМ!А, 2004.

4. Шихин А.Я. Электротехника. Москва, Высшая школа, 2001

5. Берикашвили В.Ш., Черепанов А.К. Электронная техника. Москва,

АСАДЕМ!А, 2005.

6. Трофимова Т.И., Курс физики. Москва, Высшая школа, 2003