П. 2. Изображения некоторых элементарных функций

1. Изображение единичной функции Хевисайда.

Найдем изображение, вычисляя интеграл (2):

= .

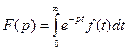Найдем показатель роста.

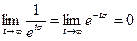, если 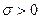, отсюда .

F(p) определена в области .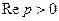

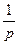Вывод: (5)

 

Преобразование Хевисайда удобно применять потому, что изображением функции будет функция .

Обычно под функцией f(t) (если не оговорено особо) понимают произведение 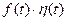, т.е. функцию тождественно равную нулю при .

 

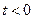2. Изображение функцииf(t) = t.

=

 

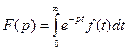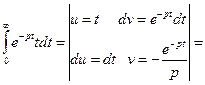
Вывод: t . (6)

3. Изображение показательной функции.

= .

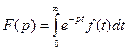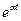
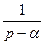Вывод: . (7)

 

Замечание. Получить изображения других элементарных функций можем аналогично, т.е. вычисляя интеграл (2), но удобнее в этих целях пользоваться общими свойствами изображений.