Теоремы подобия, смещения, запаздывания
Теорема подобия. Дополнительное умножение аргумента t в оригинале на число а  R, a > 0 приводит в изображении к уменьшению в а раз параметра p и самого изображения,
R, a > 0 приводит в изображении к уменьшению в а раз параметра p и самого изображения,
f(аt) =:  F(
F(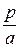 ). ( 2 )
). ( 2 )
Доказательство.
f(аt) =:  =
= 
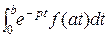 =
=  =
=
= 
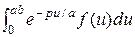 =
= 
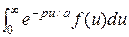 =
=  F(
F(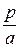 )
)
Пр.6 sin at =: 
 =
= 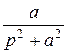 ; cos at =:
; cos at =: 
 =
=
Теорема смещения. Переход в изображении от p к (p + z), где z комплексное число, причем Re (p + z) > s0 , приводит к дополнительному умножению оригинала на экспоненту e-zt
F(p + z) =: e-zt f(t) ( 3 )
Доказательство.
e-zt f(t) =:  =
=  = F(p + z)
= F(p + z)
Пр.7 ezt sin at =: 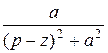 ; ezt cos at =:
; ezt cos at =: 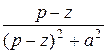
Теорема запаздывания. Уменьшение параметра t в оригинале на величину  > 0 приводит к дополнительному умножению изображения на экспоненту
> 0 приводит к дополнительному умножению изображения на экспоненту 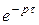
f(t - )
)  (t-
(t- ) =:
) =: 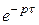 F(p) ( 4 )
F(p) ( 4 )
Доказательство.
f(t - ) =:
) =: 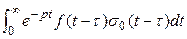 =
= 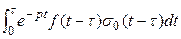 +
+
+ 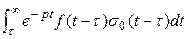
Первый интеграл равен 0, т.к.  (t-
(t- )= 0 при t<
)= 0 при t< .
.
f(t - ) =:
) =:
 =
=  =
=

 =
= 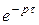
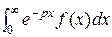 =
= 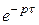 F(p)
F(p)
Пр.8  (t -
(t -  ) =:
) =: 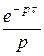 и (t – a)
и (t – a) (t - а) =:
(t - а) =:  с учетом Пр. 5 .
с учетом Пр. 5 .