Преобразование Лапласа

ББК 22.161.1

УДК 517.31

Базовые конспекты лекций

ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ

ЭЛЕМЕНТЫ ТЕОРИИ

Казанский государственный

Адреса DRAM-памяти


Следующая порция битов указывает на смещение ячейки внутри DRAM-страницы (или, говоря другими словами, представляет собой номер столб­ца). В зависимости от конструктивных особенностей микросхемы памяти длина DRAM-страниц может составлять 1, 2, или 4 Кбайт, поэтому количе­ство бит, необходимых для ее адресации, различно. Но ведь разработчики чипсетов тоже люди и реализовывать несколько систем трансляции адресов им особого удовольствия не доставляет! Большинство существующих чипсе­тов поддерживают модули памяти только с DRAM-страницами размером в 2 Кбайт, что соответствует 7 битам, отводимых для их адресации (надо учи­тывать, что адресуются не биты, а пакеты по 16 байт = 24). Более "продвинутые" чипсеты (в частности Intel 815) умеют обрабатывать страни­цы и большего размера, отображая старшие биты номера столбца в самый "конец" процессорного адреса. Таким образом, программная длина DRAM-страниц практически во всех системах равна 2 Кбайт, — и это обстоятельст­во еще не раз пригодится нам в будущем.

Следующие один или два бита отвечают за выбор банков памяти. Все моду­ли памяти, емкость которых превышает 64 Мбайт, имеют четыре DRAM- банка и потому отображают на логическое адресное пространство два бита (22 = 4).

Оставшиеся биты представляют собой номер DRAM-страницы и их количе­ство напрямую зависит от емкости модуля памяти.

энергетический университет

Кафедра «Высшей математики»

 

 

 

 

Казань 2006


 

Элементы теории операционного исчисления. Казань: Каз. гос. энерг. ун-т, 2006.

 

Работа включает краткие теоретические сведения по теме «Операционное исчисление». Вводится преобразование Лапласа, доказываются теоремы подобия, смещения, запаздывания. Вычисляются изображения основных элементарных функций. Рассматриваются простые приемы отыскания оригинала по изображению и основные правила дифференцирования и интегрирования оригиналов и изображений.

Работа предназначена для первичного знакомства студентов с базовыми понятиями и основными моментами теории операционного исчисления.

Данный учебный материал по составу и объему соответствует программам технических специальностей университета по высшей математике. Он представлен в четкой, сжатой форме, даны исходные определения и доказательства основных теорем. Это опорные конспекты лекций, на основе которых преподаватели кафедры «Высшая математика» КГЭУ организуют свои лекционные курсы по данной теме.

 

 

Авторский коллектив: Арсланов Ф.Х. , Гарифьянов Ф.Н. , Гимадиев Р.Ш. , Григорян С.А., Желифонов М.П., Липачева Е.В., Никитин А.С., Хамзин А.А.

 

© Казанский государственный энергетический университет, 2006

 

 

ЭЛЕМЕНТЫ ТЕОРИИ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ

 

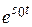Пусть функция f(t)обладает следующими свойствами: 10 f(t)0при t < 0 ; 20 | f(t)| < M при t > 0, где М > 0 , т.е. f(t) возрастает не быстрее некоторой экспоненты и s0–показатель роста функции ; 30 На любом промежутке оси [a,b]выполняются условия Дирихле – функция кусочно-непрерывна и имеет конечное число экстремумов и точек разрыва I рода.

Такие функции наз. изображаемыми по Лапласу или оригиналами. Запишем интеграл

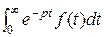=F(p)( 1 )

 

где p = s + iq - комплексная переменная. При s 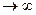и F(p) 0 . При указанных условиях он сходится и наз. интегралом Лапласа, а функция F(p) наз. изображением оригинала. Переход от f(t) к F(p) наз. преобразованием Лапласа и обозначается f(t) =: F(p) или F(p) =: f(t). Для значения f(t) в точке разрыва t0 выбирают f(t0) = ½ [f(t0 - 0) + f(t0 + 0)] . При этих условиях между f(t) и F(p) существует взаимно – однозначное соответствие.

Смысл преобразования – многим операциям над оригиналом соответствуют более простые операции над изображением. Например, решение дифференциальных и интегральных уравнений может существенно упроститься.