Решение уравнений численными методами
End.
Begin
Begin
Var
Const
Uses
End.
Begin
Var
Const
Uses
С заданным числом циклов n.
3. Блок-схема алгоритма программы (рис.14)
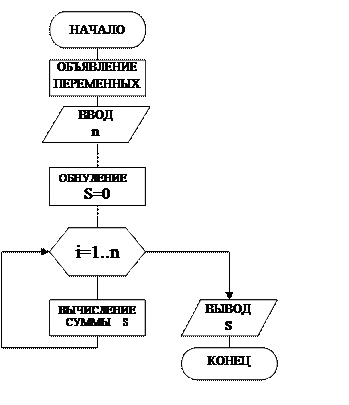
1. Начало
2. Ввод объёма массива n
3. Ввод элементов массива xiоператором цикла
4. Обнуление суммы S
5. Организация циклас заданным числом повторений n (блок цикла изображён символом шестиугольника с параметрами цикла)
6. Вычисление суммы S оператором цикла
7. Вывод результата S
8. Конец
4. Текст программы
program summa;
printer;
n = 10;{объём массива, например 10}
i : integer;{переменная цикла - целое число}
S : real;{ искомая сумма }
x : array [1..n] of real; {массив действительных чисел}
writeln (‘Введите n’);
readln (n);
writeln (‘Введите значения x[i]’);
for i:= 1 to n do {ввод циклом}
read (x[i]);
S:=0;
for i:=1 to n do {вычисление циклом}
S:= S + x[i] ;
writeln ({lst,}‘Сумма элементов ряда S=’, S:5:2);
readln;
Ввод констант и простых переменных производится обычными операторами. Для ввода массивов необходим оператор цикла с заданным числом повторений, равным объёму цикла n. Вывод результата осуществляется в заданном формате (здесь 5:2), первая цифра которого определяет общее количество знаков, включая разделитель десятичной дроби, а вторая – количество знаков этой дроби после разделителя.
Для приближённых вычислений используется оператор цикла с заранее неизвестным числом циклов. Рассмотрим для примера программу приближённого вычисления функции квадратного корня с использованием структуры ЦИКЛ – ПОКА.
ЗАДАЧА 4. Составить программу приближённого вычисления квадратного корня из заданного числа по формуле Ньютона с заданной точностью.
1.Постановка задачи
Задано: действительное положительное число xи точность eps
Найти: приближённое значение функции y = sqr (x) c
заданной точностью eps по формуле Ньютона
y2= 0.5 ( y1 + x/y1 )
2.Формализация задачи
1. Ввести значения аргумента xи точностиeps
2. Вычислить начальное приближение y1 = x/2
3.Подставить y1 в формулу Ньютона и вычислить значение y2
4. Организовать цикл вычислений по формуле Ньютона, причём на каждом шаге проверять выполнение условия
| y2 – y1| > eps
5.Цикл вычислений продолжать до тех пор, пока это условие выполняется
6. Прекратить вычисления в противоположном случае, когда разность соседних значений становится по модулю меньше точности
7. вывести последнее значение y2 как результат.
3. Блок-схема алгоритма программы (рис.15)

4. Текст программы
program radix;
printer;
eps = 0.001;
x, y1 , y2 : real;
writelen (‘Введите x = ’) ;
readln (x);
y1 : = x/2; { начальное приближение }
y2 := 0.5* (y1 + x/y1 );
while { начало цикла ПОКА }
abs (y2 –y1) > eps do { условие точности }
y1:= y2;
y2:= 0.5*(y1 + x/y1);
end; { конец цикла ПОКА }
writeln ({lst,}’Квадратный корень y =’, y:5:2);
readln;
ЛЕКЦИЯ 8
В самых разнообразных областях современной науки и техники приходится встречаться с такими математическими задачами, для которых невозможно получить точное решение классическими методами, или же решение получается в таком сложном виде, что исключает его практическое использование. К таким задачам можно отнести отыскание корней уравнений высоких степеней, решение систем дифференциальных уравнений, обработку результатов экспериментальных исследований с нахождением аппроксимирующих функций, интегрирование произвольных функций, быстрое вычисление полиномов высоких порядков и др.
С другой стороны, развитие средств современной вычислительной техники и программного обеспечения позволяет применять технологии и методы, обеспечивающие приближённое решение таких задач с заданной точностью и приемлемым быстродействием. Базовой основой этих методов является активно развивающаяся отрасль, получившая название вычислительной математики.
Установим круг вопросов, относящихся к практическому разделу вычислительной математики – методам вычислений. Для этого рассмотрим процесс решения любой математической задачи, который необходимо довести до числового результата, используя наличные вычислительные средства. Этот процесс можно разбить на два основных этапа.
Первый этап – выбор численного метода решения задачи. Он представляет собой замену исходных функций на приближённые к ним с заданной точностью функции, более удобные для вычислительных целей.
Второй этап - составление алгоритмов вычисления, компьютерных программ и выполнение самого процесса вычислений.
Для примера рассмотрим методику численного решения уравнений.
Пусть задано уравнение F(x) = 0, где F(x) – произвольная непрерывная функция. Решение уравнения означает нахождение его корня, т.е. значения аргумента x = c, подстановка которых в уравнение обращает его в нуль: F(c) = 0. Численное решение уравнения предусматривает два этапа:
1.Выбор начального приближения и подстановку его в уравнение
2.Организацию циклического процесса последовательной подстановки очередного вычисленного значения корня в уравнение до достижения заданной точности.
Обычно на первом этапе определяется целая часть корня. Далее задаётся точность решения и происходит переход ко второму этапу. Поиск начального приближения или отделение корней основан на следующей теореме:
Если непрерывная функция F(x) принимает на концах отрезка [a,b] значения разных знаков, т.е. F(a)*F(b) < 0, то на отрезке [a,b] существует корень уравнения F(x) = 0, хотя бы один (рис.16).
Физический смысл этой теоремы заключается в том, что разные знаки появляются при прохождении функции на данном отрезке через нуль.

Рис. 16 Рис. 17
Количество корней определяется по знаку производной функции F’(x). Если на заданном участке [a,b] производная F’(x) сохраняет знак, то функция монотонная и корень на заданном участке только один (рис. 17). Иногда начальное приближение можно определить заранее, исходя из физических соображений и анализа заданной функции. Если это невозможно, то в качестве начального приближения искомого корня уравнения выбирается один из концов отрезка
x0 = a, или x0 = b.
Чтобы определить правильность выбора начального приближения, можно исследовать графики функции или её производной. После выбора значений a и b следует подставить их в уравнение и проверить, действительно ли функция меняет знак. При этом вычисления могут быть приближёнными, т.к. здесь надо установить только знак функции, а величина не имеет значения.
Пример
Задано уравнение: 0,1 x2 – x*ln x = 0.