Программирование циклических алгоритмов
End.
Begin
Var
Uses
End.
Begin
Var
Uses
printer;
a,b,c,x,y,z,t:real;
writeln(‘Введите a,b,c,x’);
readln (a,b,c,x);
z:=a+b;
t:= sqr(c+a);
y:= (z/t)*cos(x);
writeln({lst,}‘При a=’, a:5:2, ‘b=’, d:5:2, ‘c=’, c:5:2, ‘x=’, x:5:2,
‘Значение функции y=’, y:7:2);
readln;
Комментарии в апострофах ‘’ и в фигурных скобках {} не участвуют в работе программы. Текст в апострофах выводится на монитор и принтер и помогает в чтении и анализе результатов работы программы, как самому пользователю, так и другим лицам.
Пустой оператор в конце программы служит для того, чтобы текст программы не закрывал результат вычислений. Если это имеет место, можно переключать экран монитора с результата на текст программы и обратно сочетанием клавиш alt+F5.
Для данной достаточно простой задачи разбиение текста на отдельные блоки не является обязательным и приведено для наглядности. Однако при сложных вычислительных формулах такой метод позволяет избежать ошибок при написании громоздких формул. Кроме того, при введении промежуточных переменных, существенно облегчается отладка программы.
Разветвляющиеся алгоритмы содержат, по крайней мере, одно условие. Для их реализации используются типовые структуры РАЗВЕТВЛЕНИЕ, программирование которых производится операторами условия. В качестве примера программирования разветвляющегося алгоритма рассмотрим следующую задачу.
ЗАДАЧА 2
Вычислить значение функции y для различных значений
аргумента xпо формуле
ax2 + b при a<=0
y =
ax2 - 2 при a > 0
1. Постановка задачи
Задано: a, b, x - действительные числа
Найти:
ax2 + b при a<=0
y =
ax2 - 2 при a > 0
2. Формализация задачи
Задача представляет собой вычисление функции по двум различным формулам в зависимости от знака заданной переменной a. Для решения используется условный алгоритм вида IF – THEN – ELSE, позволяющий переключить работу программы на одну из двух ветвей. После вычисления значения искомой функции полученный результат поступает на блок вывода и работа программы завершается.
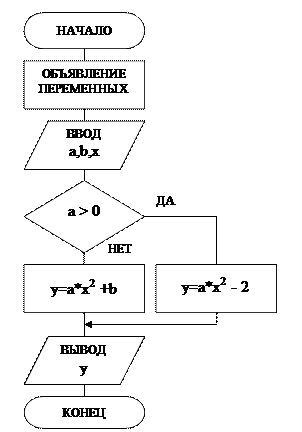
3.Блок-схема алгоритма программы (рис.13)
1. Начало
2. Объявление переменных a,b,x,y
3. Ввод данных a,b,xс клавиатуры
4. Проверка условия a > 0
4. Вычисление yпо формуле, определяемой проверкой условия
5. Вывод исходных данных и результата в выбранном формате
6. Конец
4. Текст программы
program razvet;
printer;
a, b, x : real;
writeln (‘Введите значения a, b, x’);
readln(a, b, x);
if a <= 0 then
y = a*x*x + b
else{ перед else НЕТ запятой}
y = a*x*x – 2;
writeln ({lst,}‘При a = ’, a:5:2, ‘y = ’, y:6:2);
readln;
Контрольный пример решается для двух вариантов переменной aв
соответствии с условием задачи.
ЛЕКЦИЯ 7
Циклические алгоритмы делятся, как известно, на два типа:
1. с известным числом циклов
2. итерационные, в которых условием прекращения цикла является выбранное условие (обычно достижение заданной точности вычислений).
Результатом вычислений в первом случае является точное значение параметра, а во втором – приближённое с заданной точностью, что характерно для приближённых численных методов вычислений.
Рассмотрим сначала программирование циклических алгоритмов первого типа – с заданным числом циклов n. Здесь используется типовая структура вида ЦИКЛ – ДО. Типичным примером использования этой структуры является задача нахождения суммы элементов массива.
ЗАДАЧА 3. Нахождение суммы оператором цикла
1. Постановка задачи
Задано: массив значений действительных чисел x1 ...xi....xn
объёмом n
Найти: сумму S значений массива
2. Формализация задачи
Для записи результатов вычислений необходимо выделить ячейку памяти, предварительно очистив её от находящейся в ней информации. Такая процедура называется обнулением и записывается как
S = 0;(мнемоническое правило: «ноль не портит суммы» - вытекает из
очевидного положения, что прибавление нуля к любому числу не
изменяет его величины).
Далее выполним первый шаг вычислений по рекуррентному выражению, добавляя к сумме первое значение массива x1:
1. S= S + x1 = 0 + x1 = x1
Полученное первое значение суммы S= x1 запишем в ту же ячейку S,
вытеснив оттуда нулевое.
Второй шаг:
2. S= S + x2 = (x1 + x2)
Теперь полученное второе значение запишем в ту же ячейку S,
вытеснив первое.
Третий шаг: повторим предыдущую процедуру
3. S = S + x3 =(x1 +x2 )+x3
Таким образом, рекуррентная формула на каждом шаге добавляет к сумме
очередной элемент ряда и записывает новую сумму в ту же ячейку памяти,
где хранилось предыдущее значение суммы элементов ряда.
…
n. S = Sn-1 + xn
т.е. после перебора всех nэлементов ряда в ячейке будет записано значение суммы элементов ряда S.
Для такого алгоритма применима типовая структура цикл – до