Информационные процессы и технологии
В широком смысле слово технология – это способ освоения человеком материального мира с помощью социально организованной деятельности, которая включает три компоненты: информационную (научные принципы и обоснование), материальную (орудие работы) и социальную (специалисты, имеющие профессиональные навыки). Эта триада составляет сущность современного понимания понятия технологии.
Понятие информационной технологии появилось с возникновением информационного общества, основой социальной динамики в котором являются не традиционные материальные, а информационные ресурсы: знания, наука, организационные факторы, интеллектуальные способности, инициатива, творчество и т.д.
| Процессы, связанные с получением, хранением, обработкой и передачей информации, называются информационными процессами. |
Как уже ранее говорилось, для автоматизации работы ЭВМ с информацией, относящейся к различным типам, очень важно привести информацию к определенной форме представления – для этого обычно используется прием кодирования. Большинство кодов основано на системах счисления, причем использующих позиционный принцип образования числа, при котором значение каждой цифры зависит от ее положения в числе.Система счисления – это способ записи чисел с помощью заданного набора специальных знаков (цифр).
Все системы счисления делятся на две большие группы: позиционные и непозиционные.
В непозиционных системах счисления значение цифры не зависит от позиции, которую она занимает в числе. Например, в римской системе счисления в числе XXXII (тридцать два) вес цифры X в любой позиции равен просто десяти.
В позиционных системах счисления значение каждой цифры изменяется в зависимости от ее позиции в последовательности цифр, изображающих число.
Любая позиционная система характеризуется своим основанием. Основание позиционной системы счисления – это количество различных знаков или символов, используемых для изображения цифр в данной системе.
В позиционной системе счисления число можно представить через его цифры с помощью следующего многочлена относительно q (основание системы счисления):
В позиционной системе счисления любое число можно представить в виде: 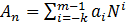
Где:ai – i–я цифра числа;
k – количество цифр в дробной части числа;
– количество цифр в дробной части числа;
m – количество цифр в целой части числа;
N – основание системы счисления.
Пример 1.3. Для десятичного числа 345 (N = 10) его полное значение рассчитывается по формуле:
А10=3*102 + 4*101 + 5*100 = 345.
Пример 1.4. Целая часть числа отделяется от дробной части точкой (запятой). Полное значение десятичного числа 37,25 (N = 10) будет представлено в следующем виде:
А10=3*101+7*100+2*10–1+5*10–2 = 37,25
В современной информатике используются в основном три системы счисления (все – позиционные): двоичная, шестнадцатеричная и десятичная.
Двоичная система счисления используется для кодирования дискретного сигнала, потребителем которого является вычислительная техника. Вся информация представляется в виде определенной последовательности нулей и единиц (0 – нет сигнала, 1 – есть сигнал): 010001110011001110111
Шестнадцатеричная система счисления используется для кодирования дискретного сигнала, потребителем которого является хорошо подготовленный пользователь – специалист в области информатики. В качестве первых 10 из 16 шестнадцатеричных цифр взяты привычные цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, а вот в качестве остальных 6 цифр используют первые буквы латинского алфавита: A, B, C, D, E, F. Цифра 1, записанная в самом младшем разряде, означает просто единицу. Та же цифра 1 в следующем – 16 (десятичное), в следующем – 256 (десятичное) и т.д. Цифра F, указанная в самом младшем разряде, означает 15 (десятичное).
Десятичная система счисления используется для кодирования дискретного сигнала, потребителем которого является так называемый конечный пользователь – неспециалист в области информатики (очевидно, что и любой человек может выступать в роли такого потребителя). Пришла в Европу из Индии, где она появилась не позднее VI века н.э. Соответствие между первыми несколькими натуральными числами всех трех систем счисления представлено в таблице перевода:
| Десятичная система | Двоичная система | Шестнадцатеричная система |
| A | ||
| B | ||
| C | ||
| D | ||
| E | ||
| F | ||
Перевод целых чисел в другие системы счисления.Целое число с основанием 10 переводится в систему счисления с основанием 2 путем последовательного деления числа, на основание 2 до получения остатка. Полученные остатки от деления и последнее частное записываются в порядке, обратном полученному при делении. Сформированное число и будет являться числом с основанием N2.
Пример 1.5. Выполнить перевод десятичного числа А10 =37 в двоичную (А2 =?) и шестнадцатеричную систему счисления (А16 =?)

Перевод дробных чисел в другие системы счисления.Целое число с основанием 10 переводится в систему счисления с основанием 2 путем последовательного умножения числа, на основание 2. Целая часть записывается в дробное число в той последовательности, в которой получалась. Сформированное число и будет являться числом с основанием N2.
Пример 1.6. Выполнить перевод десятичного числа А10 =0,847 в двоичную (А2 =?) и шестнадцатеричную систему счисления (А16 =?)

Перевод чисел в десятичную систему осуществляется путем составления многочлена относительно q (основание системы счисления), из которой число переводится. Затем подсчитывается значение суммы.
Пример 1.7. Выполнить перевод двоичного числа А2 = 100101 в десятичную систему счисления (А10 =?) и шестнадцатеричного числа А16 = 25,D8 в десятичную систему счисления (А10 =?)
| Воспользуемся формулой (1.1): А10 =1*25 + 0*24 + 0*23 + 1*22 + 0*21 + 1*20 = 32+0+0+4+0+1 = 37 |
| Итак, А2 = 100101 в десятичной системе выглядит следующим образом: А10 = 37 |
| Воспользуемся формулой (1.1): А10 =2*161+ 5*160+ 13*16–1 + 8*16–2 = 32+5+0,81+0,031= 37,84 |
| Итак, А16 = 25,D8 в десятичной системе выглядит следующим образом: А10 = 37,84 |
Кодирование текстовых данных. Если каждому символу алфавита задать целое число, то можно с помощью двоичного кода кодировать текстовые данные. Восьми двоичных разрядов достаточно для кодирования 256 различных символов. Этого хватает, чтобы закодировать все строчные и прописные буквы английского или русского алфавита, а также знаки препинания, цифры, символы основных арифметических операций и некоторые специальные символы, например «%».
| При двоичном кодировании текстовой информациикаждому символу ставится в соответствии своя уникальная последовательность из восьми нулей и единиц, свой уникальный двоичный код от 00000000 до 11111111 (десятичный код от 0 до 255). |
Технически это просто, но существуют организационные сложности. Для того чтобы весь мир одинаково кодировал текстовые данные, нужны единые таблицы кодирования, а это трудно осуществить из-за использования различных символов в национальных алфавитах. Сейчас по ряду причин наибольшее распространение получил стандарт США ANСII (American National Code for Information Interchange) – Американский национальный код для обмена информацией. В системе кодирования ANСII закреплены две таблицы кодирования: базовая со значениями кодов от 0 до 127 и расширенная с кодами от 128 до 255.
Коды от 0 до 31 базовой таблицы содержат так называемые управляющие коды, которым не соответствуют символы языка. Они служат для управления устройствами ввода-вывода. Коды с 32 по 127 служат для кодирования символов английского алфавита, знаков препинания, цифр и некоторых других символов. Расширенная таблица с кодами от 128 до 255 содержит набор специальных символов.
Аналогичные системы кодирования разработаны и в других странах. В России большое распространение имеет код КОИ-8.
Трудности создания единой системы кодирования текстовых данных связаны с ограниченным набором кодов (256). Если кодировать символы не 8-разрядными двоичными числами, а 16-разрядными, это позволит иметь набор из 65 536 различных кодов. Этого достаточно, чтобы в одной таблице разместить символы большинства языков. Такая система кодирования называется Unicode – универсальный код. Переход к этой системе долго сдерживался из-за недостатка памяти компьютеров, так как в системе Unicode все текстовые документы становятся вдвое длиннее. В настоящее время технические сложности преодолены и происходит постепенный переход на универсальную систему кодирования.
Кодирование графической информации. Общепринятым сегодня считается представление черно-белых иллюстраций в виде комбинации точек с 256 градациями серого цвета. При этом для кодирования яркости любой точки достаточно 8-разрядного двоичного числа.
Для кодирования цветных графических изображений применяется принцип декомпозиции произвольного цвета на три основных – красный, зелёный и синий. Для кодирования яркости каждой составляющей используется 256 значений (8 двоичных разрядов). Для кодирования цвета используются 24 разряда. Такая система кодирования обеспечивает представление 16,5 млн различных цветов.
Графический режим вывода изображения на экран определяется разрешающей способностью экрана и глубиной цвета. Полная информация о всех точках изображения, хранящаяся в видеопамяти, называется битовой картой изображения.
Кодирование звуковых данных.Звуковой сигнал – это непрерывная волна с изменяющейся амплитудой и частотой. Чем больше амплитуда сигнала, тем он громче для человека, чем больше частота сигнала, тем выше тон. Для того чтобы компьютер мог обрабатывать непрерывный сигнал, он должен быть дискретизирован., т.е. превращен в последовательность электрических импульсов (двоичных нулей и единиц). При двоичном кодировании непрерывного звукового сигналаон заменяется серией его отдельных выборок – отсчетов.
Каждая выборка фиксирует реальную амплитуду сигнала и присваивает ей определенное, наиболее близкое, дискретное значение. Чем большее количество дискретных значений может обеспечить звуковая карта и чем больше количество выборок производиться за 1 секунду, тем точнее процедура двоичного кодирования.
Современные звуковые карты могут обеспечить кодирование 16777216 различных уровней сигнала или состояния. Для определения количества бит, необходимых кодирования, можно определить из уравнения:
16777216 = 2I, т.к. 16777216 = 232, то I = 32 бита.
Таким образом, современные звуковые карты обеспечивают 32-битное кодирование звука. При каждой выборке значению амплитуды звукового сигнала присваивается 32-битный код.
Количество выборок в секунду может быть в диапазоне от 8000 до 48000, т.е частота дискретизации аналогового звукового сигнала может принимать значение от 8 до 48 Гц. При частоте 8 кГц качество дискретизированного звукового сигнала соответствует качеству радиотрансляции, а при частоте 48 кГц – качеству звучания аудио-CD. Следует тГц качество дискретизированного звукового сигнала соответствует качеству радиотрансляции, а при частоте 48 кГц – качеству звучания аудио-CD. Следует также учитывать, что возможности как моно-, так и стерео-режимы.
Можно оценить информационный объем моноаудиофайла длительностью звучания 1 секунду при среднем качестве звука (16 бит, 24 кГц). Для этого количество бит на одну выборку необходимо умножить на количество выборок в секунду:
16 бит * 24000 = 384000 бит = 48000 байт » 47 Кбайт
Практикум по решению задач. Тема: «Данные и информация»