Сигналдарды топтастыру

Сигналдарды топтастыру олардың математикалық моделдерге сәйкестік белгілеріне қарай жүзеге асырылады. Барлық сигналдар аударылған және кездейсоқ екі ірі топқа бөлінеді.

Ақпарат және сигналдарды беру теориясында ақпарат ретінде оларды кеңістік пен уақытта беру аспектісінде қарастырылатын қандай да бір оқиғалар, процестер, оқиғалар туралы мәліметтер жиынын түсінеді.

Ақпаратты хабарлама түрінде береді. Хабарлама деп көзден адресатқа жіберуге арналған және білгілі бір формада көрсетілген ақпаратты айтады. Хабарлама мысалы ретінде мыналар бола алады: телеграмма мәтіндері, сөз, музыка, телевизиялық бейне, компьютердің шығысындағы деректер, обьектілерді автоматты түрде басқару жүйесіндегі командалар және т.с.с. Хабарламаны ақпаратты тасығыш болып табылатын сигналдар көмегімен береді. Сигналдардың негізгі түрі электрлік болып табылады. УКейінгі кезже оптикалықь сигналдар кең таралуда мысалы, ақпаратты талшықты-оптикалық беру желісінде.

Ақпарат теориясында ақпаратты сигнал көмегімен қашықтыққа беру кезінде орын алатын процестердің қасиетін зерттейді. Сонымен қатар ақпаратты беру жылдамдығы мен сапасы түсініктері маңызды мәнге ие.

Ақпаратты беру сапасы неғұрлым жоғары болса, қабылдау шы жақтағы ақпараттың өзгерісі соғырлым аз болады. Ақпаратты беру жылдамдығының аруына байланысты ақпараттың жоғалуы және сапасының төмендеуіне қарсы арнайы шаралар қабылдау керек.

Ақпараттық жүйенің обьектілері

Функционалдық тағайындалуына байланысты ақпараттық тенхниканың негізгі кластарын бөліп қарастыруға болады:

желілер, байланыс жүйелері және телекоммуникациялар (телеграфтық, телефондық, телевизиялық, компьютерлік және т.б.);

ақпараттық-өлшеу жүйелері0 (радионавигациялық, радиолокациялық, телеметрикалықжәне т.б.);

ақпаратты түрлендіру жүйелері (аналог-сандық, сандық-аналогтық түрлендіргіштер, сандық компьютерлер және т.б.);

ақпараттық-іздеу жүйелері және деректер базалары негізінде ақпаратты сақтау жүйелері;

обьектілерді эксперименталді бақылау және басқару жүйелері.

Ақпаратты беру жүйесінің жалпыланған схемасы 1-суретте көрсетілген.

 

 

1-сурет. Ақпаратты беру жүйесінің құрылымдық схемасы

 

Беруші бастапқы хабарлама A(x)-ны x1(x) сигналына түрдендіреді, мұндағы x – тәуелсіз айнымалы. Хабарламалар мен сигналдар уақытқа байланысты жиі қарастырылады. Байланыс линиясының ролін кез келген физикалық орта орындай алады (ауа, өткізгіз, оптикалық талшық). Келергілр әсерінен өзгеріске ұшыраған сигнал x2(x) қабылдағышта хабарламаның көшірмесіне түрленеді B(x). Ол мүмкіндігінше оригинал A(x)-қа жақын болуы керек.

Көп арналы ақпаратты беру жүйесі бір ғана байланыс желісі бойынша бір мезгілде және өзара тәуелсіз хабарлама беруді қамтамасыз етеді. Ондай жүйенің құрылымдық схемасы 2- ші суретте көрсетілген.

 

2-ші сурет.

 

ИС, ПС – хабарлама көзі мен алушысы, К – кодерлер, М- модуляторлар, Дк- декодерлер, Дм-демодуляторлар.

Байланыс түйіні (ақпараттық түйін) неғұрлым күрделі жүйе болып табылады, себебі көпарналы ақпаратты берумен қатар келесілерді қамтамасыз етеді:

Хабарламаның көзі мен алушының арасында қысқа жолды таңдау;

Приоритеттер жүйесін сақтау;

Бос арналар болмаған кезде ақпаратты жинау мен сақтау;

Барлық көрсетілген функцияларды автоматты режимде компьютермен басқару.

Ақпараттық желі байланыс линиялары көмегімен қосылған ақпараттық түйіндер жиыны болып табылады.

3-ші суретте ақпараттық желі графының мпысалы көрсетілген.

Графтың төбелері gi, i=1,…,n, ақпарат түйіндерін білдіреді, доғалар-байланыс линиялары, олардың координаталары qij болып өткізу қабілеті, хабарлама ағынының интенсивтігі, арна құны және тағы басқалар табылады.

Ақпараттық жүйені бұқаралық қызмет көрсетудің желілік жүйесі ретінде қарастырады. Ақпараттық желілерді құру кезінде анализ, синтез және оңтайландыру есептерін шешу қажет. Есептердің негізгі кластары мыналар:

- хабарлама көздерінің ақпараттық сипаттамасының анализі;

- сигналдармен кедергілердің анализі мен синтезі;

- ақпаратты беру әдістерінің кедергіге төзімділігінің анализі мен синтезі;

- ақпаратты беру әдістерінің кедергіге төзімділігінің анализімен синтезі;

- корректерлеуші кодттардың анализі мен синтезі (қателерді табу мен түзету);

- ақпаратты беру арналарының анализінің синтезі.

 

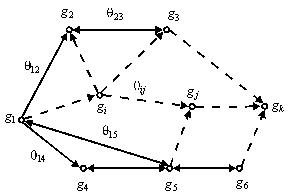
3-ші сурет.

 

Ақпараттық жүйелердегі хабарлама түрлері

Дискретті хабарлама жеке символдардың соңғы тізбегі болып табылады. Дискретті хабарламаны сигналға түрлендіру үшін хабарламаны кодтау операциясын орындау керек, сол кезде ақпаратты беру жылдамдығы мен кедергіге төзімділігі артады.

Үздіксіз хабарлама уақыттың үздіксіз функциясымен анықталады. Үздіксіз хабарламаларды дискретті әдістермен беруге болады. Бұл үшін үздіксіз сигналды (хабарламаны) уақытта дискреттеу мен деңгей бойынша кванттауға ұшыратады. Қабылдаушы жақта дискретті есептеулер бойынша үздіксіз фуекцияны қалпына келтіру орындалады.

Хабарламаны математикалық түрде сипаттау кезінде дискреттік хабарламалардың құрылуы хабарлама көзінің алфавитінен кез келген символды кездейсоқ тізбектей таңдау ретінде қарастырылады.

Үздіксіз хабарламалардың құрылуы кездейсоқ үздіксіз процестің іске асырылуын (реализация) таңдау болып табылады. Негізгі ақпараттық сипеаттамаларға хабарламалардағы ақпарат саны, хабарлама шығындығы, энтропия, хабарлама көзінің шығару мүмкіндігі, ақпаратты беру жылдамдығы жатады.

Аталған сипаттамаларды дискретті хабарлама үшін қарастырайық.

Ақпарат көлемі A, m дискретті хабарламадан тұрсын, әр хабарлама n символ кірсін. Қабылданған белгілеулерде дискретті символдардың жалпы саны N0=mn болады. Осындай көздердегі хабарламаларда ақпарат саны қалай анықталатынын көрсетейік.

Ақпарат санын анықтау кезінде келесі шарттар орындалуы керек:

- ұзақ созылған хабарламаларда әдетте, ақпарат саны көп болады;

- егер алфавит көлемі үлкен болса, онда әрбір жеке хабардамада ақпарат көбірек болады;

- бірнеше хабарламада алынған ақпарат аддиттивтік шартын қанағаттандыру керек.

Хабарламалардың жоғарыда көрсетілген шарттарда қанағаттандыратын ыңғайлы сипаттамасы ақпарат санының логарифмдік өлшемі І болады, нақтырақ айтсақ.

 

I = logN0=nlogm.

Бұл формуланы 1928 Р.Хартли ақпарат санының өлшемі ретінде ұсынған. Хартли формуласы хабарламалар құрылуының кедейсоқ сипатын көрсетпейді. Бұл кемшілікті жою үшін хабарламадағы ақпарат санын символдардың пайда болу ықтималдығымен байланыстыру керек. Бұл мәселені 1948 ж К.Шеннон шешті.

Ақпарат санын анықтау

Хабарлама бір символдан тұрсын дейік. Егер барлық символдардың пайда болу ықтималдығы бірдей және P = 1/m болса, онда символдың тасымалдайтын ақпарат санын былай көрсетуге болады

 

I1 = log m = -log P.

 

Мұнда ақпарат саны символдың пайда болу ықтималдығымен байланысты. Шынайы хабарламаларда символдар ai Î A әртүрлі ықтималдықтармен пайда болады P(ai), сондықтан

 

Ii = -log P(ai).

 

Хабарлама көзінің бір символына сай келетін ақпараттық орта саны алфавиттің барлық көлемінің орташа мәні арқылы табуға болады.

 

H(A) = - . (1)

 

Бұл шама дискреттік хабарламаның энтпропиясы деп аталады. (1) формула Шеннон формуласы деген атқа ие.

Энтропия хабарлама көзінің іс-әрекетіндегі анықталмағандықтың мәні ретінде қарастырылады. Ықтмиалдық тәсілімен келгенде ақпарат көзінің күйі анйқталмағандықпен сипатталады. Анықталмағандық хабарламаны қабылдау кезінде, яғни ақпарат алғанда азаяды. Сондықтан хабарлама көзінің бір символына келетін, алынатын ақпарат анықталмағандық деңгейін сан түрінде анықтайды. Энтропия символдардың пайда болу ықтималдығынан үздіксіз функция болып табылады және келесі қасиеттерге ие:

- дискретті хабарламалар көзінің энтропиясы заттық шама, шектеулі және теріс емес;

- егер бірлік ықтимаплдығымен бір ғана символ таңдалса, энтропия 0-ге тең (көздің әрекетінде анықталмағандық жоқ);

- егер көздің барлық символдары тәуелсіз және бірдей ықтималдықпен пайда болса, онда энтропия максималды:

 

Hmax = mPlogP = m(1/m)log(1/m) = log m.

 

Егер символдар өзара байланысқан болса, онда шартты энтропия түсінігі қолданылады.

H(A’/A) = - , (2)

 

Мұнда, P(aj’/ai) – ai символынан кейінгі aj символының пайда болуының шартты ық тималдығы.

Символдарың корреляциялық байланысы мен шынайы хабарламаларда олардың пайда болу ықтималдығының теңсіздігінен бір символдың тасымалдайтын ақпараттың орташа саны азаяды. Бұл жоғалтулар шығындылық коэффициентімен сипатталады.

R=(H1-H)/H1=1-H/log m,

 

H1– бір символ тасымалдай алатын ақпараттың максималды саны, H – бір символдың шынайы хабарлама тасымалдайтын ақпарат саны (мысалы, европалық тілдер үшін r≥0,5 ).

Логарифм негізін (1)-де көбінесе 2-ге тең деп алады. Бұл жерде ақпарат санының өлшемі бит болып табылады (binary digit).

Хабарлама көзінің шығару қабілеті деп көздің уақыт бірлігіндегі беретін ақпараттың орташа санын атайды, дәлірек айтқанда

H’ = H/t [бит/с].

Ақпаратты беру арналары үшін аналогтық сипаттаманы енгіземіз, ол С – ақпаратты беру жылдамдығы. Оның максималды шамасы арнының өткізу қабілеттігі деп аталады. Дискретті арна үшін.

C=V∙ log m [бит/с], (3)

Мұнда V– электрлік коддықсигналдарды беру жылдамдығы.

Дискретті хабарлама көздерінің ақпараттық сипаттамалары

Символдардың пайда болу ықтималдығының теңсіздігі мен олардың арасындағы өзара байланысты ескере отырып шартты энтропия қасиетін қарастырайық.

Қарапайымдылық үшін ai символының пайда болуы алдыңғы aj символының қандай болғанына ғана байланысты деп алайық (хабарламаның құрылу процесі – Марковтың қарапайым тізбегі). Екі символдың бірге пайда болу энтропиясы

H(A, A’) = , (4)

Мұндағы P(ai,aj’) – ai және aj’ символдарының бірге пайда болу ықтималдығы. aiaj’ буынына келетін ақпарат саны log P(ai,aj’)-ға тең.

P(ai,aj/)=P(ai) P(aj//ai), екенін ескере отырып,

 

H(A, A’) = -

= - (5) деп жазамыз.

Нормалау шарттарын ескере отырып

,

 

екі символдың бірге пайда болу энтропиясы ұшін соңғы мәнді мына түрде жазамыз

H(A, A’) = H(A) + H(A’/A), (6)

Мұндағы H(A) – (1)-де анықталған және (5)-тегі бірінші слагаемому сәйкес келетін көздің энтропиясы, H(A’/A) – (2) мәнімен анықталатын көздің шартты энтропиясы.

Біріккен екі символдың тасымалдайтын ақпараттың орташа саны олардың біріншісі тасымалдайтын ақпараттың орташа саны мен біріншісіеің пайда болуынан кейін екіншісінің тасымалдайтын ақпараттың орташа санының суммасына тең болады.

Шартты энтропия дегеніміз алғашқысы белгілі болу шартындағы келесісінің тасымалдайтын орташа ақпарат саны болып табылады:

H(A’/A) = H(A, A’) - H(A).

Егер ai және aj’ символдары өзара байланысты болса, онда H(A’/A) < H(A’). Символдары тәуелсіз көздер үшін

H(A, A’) = H(A) + H(A’).

Корреляциялық байланыстар символдар арасында болдуы мүмкін (L+1) онда көз жады L символға тең болады.

Екілік ақпарат көздерінің қасиеттері

Көздің символдары a1, a2 (m = 2), олардың пайда болу ықтималдығы P(a1), P(a2) болсын. Шартты ықтималдықтарды P(a1/a1’), P(a2/a2’), P(a1/a2’), P(a2/a1’) деп белгілейік.

Ықтималдықтары тең емес тәуелсіз символдар жағдайы

Ықтималдықтары P(a1)=P(a2)=P=1/2, шартты ықтималдықтары нөлге тең. Ондай көздің энтропиясы максималды болады:

 

Hmax =-(1/2)log(1/2) -1/2)log(1/2) log2 = 1 бит/симв.

 

Осылайша, 1 бит – бұл екілік хабарлама көзі тасымалдайтын ақпараттың орташа максималды саны.

Ықтималдықтары тең емес тәуелсіз символдар жағдайы

Ықтималдықтары P(a1)=P, P(a2)=1-P, шартты ықтималдықтар нөлге тең. Мұндай көздің энтропиясы манаған тең болады

H(P) = -PlogP-(1-P)log(1-P). (7)

 

2.4 суретте (7) тәуелдігі көрсетілген. Энтропия максимумы P=1/2 табылады. P≠1/2 болса, H(P)<Hmax болатындықтан, мұндай көздің шығарну қабілеттігі максималддан аз болады. Шығындылығы

 

r(P)=1-H(P)/Hmax≥0.

 

Мысал: P(a1)=0,125; P(a2)=0,875 болсын. Онда H(P)=-0.125log0.125-0.875log0.875≈0.576 бит/симв, r(P)=1-0.576 ≈0.42

 

4-сурет

 

Тең ықтималдықты коррелированных символдар жағдайы

P(a1)=P(a2)=P=1/2 болсын, шартты ықтималдықтары нөлден өзгеше және P(a1/a1’)= P(a2/a2’), P(a1/a2’)=P(a2/a1’) болсын. (2) қатынасты ескергендегі шартты энтропия мынаған тең болады:

 

H(A/A’) = -P[P(a1/a1’)log P(a1/a1’)+ P(a2/a1’)log P(a2/a1’)]-

-P[P(a2/a2’)log P(a2/a2’) + P(a1/a2’)log P(a1/a2’)]=

= -2P[P(a1/a1’)log P(a1/a1’) + P(a2/a1’)log P(a2/a1’)].

 

Мысалы, егер P(a1/a1’)=0.7, P(a1/a2’)=0,3, то H(A/A’) = -(1/2)[0.7×log0.7-0.31×log0.31] ≈ 0.88бит/симв, r = 1-0.88=0.12

Екілік көздің коррелирленбегендегі тең ықтималдықты символдардың энтропиясы 1 бит/симв – ға тең. Сәйкесінше символдар арасында статистикалық байланыстардың болуы энтропияның азаюы мен шығындылықтың көбеюіне әкеледі.

 

Тақырып 12. Деректерді жіберу желісі.

Мақсаты: қорларды тарату есебі мысалында статистикалық модель тұрғызу.

Жоспар (1 сағат)

1. Байланыс желісінің өткізу мүмкіндігі.

2. Статикалық маршрутизация есебін шығару әдісі.

Кілттік сөздер: маршрутизация, статикалық, теорема, кодтау, хабарлама, жіберу.

Жүйелік талдау үшін көп дамығаны сызықтық бағдарламалау әдістері болып табылады. Олар қорларды, рационалды орналастыру жүйелерін, шешімдерді қабылдау жүйелерін, экономикалық жүйелерді және т.б. модельдеу жолымен өндірістік, коммерциялық және басқа шешімдерді шешу кезінде қолданылады.

Бүтіндей алғанда, жүйелердің жұмысына ықпал ететін көрсетушілердің және параметрлердің көп санына байланысты тек сезім ғана жеткілікті емес.

Ақпаратты қолмен өңдеу көп еңбек шығынын талап етеді және адамдық қорлармен шектелген.

Сызықтық бағдарламалық модельдер коммерциялық және өңдірілген жүйенің эффектілі және терең талдауын жүргізуге мүмкіндік береді.

Сызықтық класстың моделін мыналарға бөлуге болады:

- Статикалық,

- Динамикалық,

- Транспорттық.

Статикалық модельдер алдын – ала анықталған уақыт интервалы үшін басқарылатын шешімдерді талдайды.

Динамикалық модельдер уақыттың мультиуақытты интервалы үшін жоспарлау тапсырмасын шешеді, басқаша айтқанда уақытысында өзгеретін параметрлердегі тапсырмалар.

Транспорттық тапсырмалардың әдістерін шешу кезінде қолданылатын модельдер, динамика элементімен статикалық тапсырмалар комбинациясын ұсынады.

Тапсырмаларды шешуге сол және басқа жақындауды операциялық түрде ұсынуға болады, ол келесі элементтерді қамтамасыз ету керек:

1. шешімдерді қабылдаудағы

2. экономикалық эффектілік критерийлерінің негізінде баға;

3. математикалық модельдерге сенім;

4. ЭЕМ қолдануды қажет ету.

 

Қорларды орнату тапсырмасы

Бірқалыпты емес өнімді шығаратын кәсіпорында тапсырылған уақыт аралығында әр өнім үшін өндіру деңгейін анықтау қажет. Өндіру деңгейі келесі шектеулерді қамтамасыз етеді:

- Технологиялық,

- Шикілік,

- Адамдық және т.б. сызықтық сәйкестікпен тапсырылған.

Осы шектеулердің ішінде мақсаттық функцияны оңтайландыру қажет.

Негізгі мақсаты – максималды пайданы алу.

Фирма 1 – 4 технологиялық процессті жүзеге асырады делік. Технологиялық процесстер 1 және 2 А өнімін шығаруға, 3 және 4 В өнімін шығаруға бағытталған.

Әрбір технологиялық процесстің еңбек шығындарымен, Y және Z материалдарын апталық тұтынумен анықталады.

Әр түрлі технологиялық процесіндегі шығындар бірдей емес болғандықтан, процесстердің пайдалылығы әр түрлі болады.

Бір аптаға өндірістік жоспар құру кезінде келесі өндірістік – экономикалық көрсеткіштерді және шектеулерді қосайық:

Кесте 1

	А өнімінің 1бірлігінде	В өнімінің 1бірлігінде	Барлығы
Т.п. 1	Т.п. 2	Т.п. 3	Т.п. 4
Аптадағы адам саны					15
Y Материалының саны (кг)					120
Z материалының саны (жәшіктегі)					100
Өнімнің 1бірлігінен пайда (тг)					max
Шығатын өнімнің көлемі	X1	X2	X3	X4

 

Ары қарай модельдің сызықтығын қамтамасыздандыратын өндірістің технологиясына байланысты өткізуді қабылдау қажет. Оларды сызықтың аксиомасы деп атайық.

1. Бөлінгіштік.Әрбір т.п. үшін әрбір пайдаланушы қорлардың ішінен соммалық пайдалану және түскен пайда шығатын өнімнің көлеміне пропорционал болады.

а) басқаша айтқанда т.п. көрсеткіштерін, олардың қарама – қайшы пропорционалдығын сақтау кезінде көбейтуге немесе азайтуға болады.

Х1 өнімнің 10 бірлігін шығару үшін, 10 адамдық – апта, Y материалының 70 бірлігі, Z материалының 30 бірлігі қажет. Кіріс 40 бірлікті құрайды.

б) барлық өндірістік – экономикалық көрсеткіштер бүтін сандық және заттық мағыналарды қабылдауы мүмкін.

2. Аддивтілік.Егер басқарушы ауыспалы Xj әрбір мағынасы анықталған болса, онда пайдаланылған қорлардың әрбір толық саны барлық т.п. реализациясы кезінде шығындалған біраттық қорлардың соммасына тең, ал толық түскен пайда барлық т.п. пайдасының соммасына тең.

Нақты жағдайларда мұндай бекітуді тек жақыннан ғана қабылдауға болады.

Қарастырылатын мысалда құруға болатын барлық 3 теңсіздікті санаймыз, сызықтық сәйкестікпен тапсырылады:

4х1+5х2+9х311х4=max(1)

1х1+1х2+1х3+1х4=<15 (адамдық – апта саны)

7x1+5x2+3x3+2x4120 (Yматериалының бірлігі) (2)

3x1+5x2+10x3+15x4 100 (Z материалының бірлігі)

(1) – теңдігі 1 – кестедегі өндірістік – технологиядық процесстің соммалық пайданы анықтайды.

(2) – теңдігі соммалық еңбекшығындарды, Y және Z материалдарын тұтынуды анықтайды. Қосымша шектеулерді қосу керек:

х10, х2 0, х3 0, х4 (3)

(1), (2), (3) – сәйкестіктерді қанағаттандыратын х1, х2, х3, х4 басқарушы ауыспалылардың анықтамасына негізделген.

(2) – шектеулерін бастау үшін шекті мағыналарды қосайық. Сонда тапсырманың формальді жазбасы мына түрде болады:

4x1+5x2+9x3х4= max (1')

1x1+1x2+1x3+1x4=15 (адамдық – апта саны)

7x1+5x2+3x3+2x4=120 (Yматериалының бірлігі) (2)

3x1+5x2+10x3+15x4=100 (Z материалының бірлігі)

xj>=0 (j=1,n) (3')

Үлкен коэффициенті мақсат функциясына кіретін ауыспалылардың максималды мағыналарын анықтаймыз. Олар мақсат функциясының мағынасына ықпал етеді.

(2) – ден х1=х2=х3=0, х4=15; х4=60; х4=66 шарттары бойынша.

Байқау мағынасы х4=60, ц.ф.=11*60=660

Шарты бойынша х1=х2=х4=0, х3=15; х3=40; х3=10.

Байқау мағынасы х3=40, ц.ф.=9*40=360

Шарты бойынша х1=х3=х4=0, х2=15; х2=24; х2=20.

Байқау мағынасы х2=24, ц.ф.=5*24=120

Шарты бойынша х2=х3=х4=0, х1=15; х1=17.1; х1=33.3.

Байқау мағынасы х1=33.3, ц.ф.=4*33.3=133.2.

Алдын – ала талдаудан мақсат функциясына х4 және х3 ықпал ететіні көрінеді, өйткені олар байқау мағынасы кезінде мақсат функциясына көп мағына береді.

Xj түрлі комбинацияларын таңдағанда мақсат функциясының мағыналары максимал мағыналарға ұмтылатын комбинацияны табуға болады. Бірақ мұндай әдіс еңбекке сыйымдылырақ және ұзағырақ.

Басқарушы ауыспалылар мағыналарының оңтайлы сәйкестігін (2) жүйесіндегі ауыспалыларды шығару әдісімен немесе Гаусс әдісімен табуға болады.

Оңтайлы шешімді х1 және х2 нөлдік мағыналарында х3 және х4 комбинацияларымен табуға болады.(2) – ден

х3+х4=15-х1-х2 (4)

3х₃+2х₄=120-7х₁-5х₂ (5)

10х₃+15х₄=100-3х₁-5х₂ (4)

(6) – дан х3 – ті алып тастаймыз. Бұл үшін (4) – ті көбейтеміз 10 – ға және (6) – дан кемітеміз.

5х₄= -50+7х₁+5х₂ (7)

(7) – де х4 бойынша коэффициентті нөмірлейміз.

х₄= -10+7/5 х₁+х₂ (8)

(5) – тен х4 алып тастаймыз. Бұл үшін (8) – ді екіге көбейтіп, (5) – тен кемітеміз.

3х₃=140-49/5х₁-7х₂ (9)

(9) – да х3 бойынша коэффициентті нөмірлейміз.

х₃=140/3-49/5х₁-7/3х₂ (10)

(10) – нан х1=х2=0; х3=140/3=46.6 бойынша х3=40 байқау мағынасын көбейтеді.

(8) – ден х4=-10 шектеумен қарсы болған.

х1, х4 басқарушы ауыспалылар үшін:

х₁+ х₄=15 - х₂ - х₃

7х₁+ 2х₄=120 - 5х₂ - 3х₃

3х₁+ 15х₄=100 - 5х₂ - 10х₃

Гаусс әдісімен жүйеге келтіреміз:

х₁+ х₄=15 - х₂ - х₃

х₁= 18 - 3/5х₂ - 1/5х₃

х₄=55/12 - 1/6х₂ - 7/12х₃

х2=х3=0 – дан х1=18; х4=4.6; мақсат функция=4*18+11*4.6=122.6

Мақсат функциясының мағынасы өскен кездегі басқарушы ауыспалылардың мағыналарының анықтамасы шешімнің жақсаруы болып саналуы мүмкін.

 

 

Тақырып 13. Кодтау теориясының жалпы түсінігі.

Мақсаты:қарастыру.

 

Жоспар (1 сағат)

1. Шеннонның кодтау туралы фундаменталды теоремасы.

2. Аналогтық-кодтау түрлендіргіші.

3. Тиімді кодтау.

Кілттік сөздер:кодтау,түрлендіргіш, көпше, алгоритм, таңба, сығу, вектор.

С – каналының өткізуші қабілеттілігі мына түрде анықталады:

C=VmaxH, (1)

V – электрлі кодтық сигналдарды жіберу жылдамдығы, H – хабарлама энтропиясы.

Каналды қолдану коэффициенті

η=V/C, 0≤η≤1,(2)

Болғандықтан 0≤V≤C.

Идеалды дискретті каналдар.

Кодшы жіберу символдарының электрлі кодтық сигналдарына ауысуын қамтамасыз етеді. Идеалды каналда кодтық сигналдар элементтерінің арасындағы кіру және шығу кезінде бірмәнді сәйкестік бар (каналда қателер жоқ). Ақпаратты жіберу жылдамдығы кодшының өнімділігіне тең:

Ck=VkHk [бит/с], (3)

Vk=1/L – элементарлы кодтық сигналдарын жіберу жылдамдығы [бит/с], Hk – кодшы энтропиясы [бит/сигн.], L – элементарлы кодтық сигналының ұзақтығы.

Идеалды каналдың өткізуші қабілеттілігі:

C=Vmax=Vklogmk, (4)

mk – кодтың негізі. Өткізуші қабілеттілігі каналдың шекті мінездемесі болып табылады. Егер кодтың негізі mk-ға тең және бір элементарлы кодтық сигналын жіберу үшін L – уақыты қажет болса, онда сигналдардың n – ұзындығымен кодтық комбинациясын жіберу үшін T=nL уақыт қажет болады. T – ұзақтығы мен кодтық комбинациясының жалпы саны N(T)=mkn тең.Сондай – ақ, бір кодтық комбинациясында ақпараттың максималды мөлшері Hmax=nlogmk. Өткізуші қабілеттілік тең:

(5)

Сондықтан идеалды дискретті каналдың өткізуші қабілеттілігі толығымен сигналдарды жіберу жылдамдығын және кодтың негізін анықтайды.

Идеалды дискретті канал үшін Шеннон теоремасы: егер дискретті каналда қателер болмаса, С – ға жақын, V – орташа жылдамдықпен ақпаратты жіберу үшін көздердің шығу кезінде хабарламаны кодтауға болады. V>C ақпаратты жіберу мүмкін емес.

Бұл теорема оңтайлы, эффектілі кодтарды құру үшін теориялық негіз ретінде қызмет етеді.

 

Санды – аналогтық қайта құру немесе аналогты – кодтық қайта құрулар екілік код түрінде берілген сандарды қайта құру үшін арналған. Санды – аналогтық қайта құрулардың схемотехникасы әр түрлі. 26.1. – суретінде схемотехникалық белгілер бойынша ЦАП классификациялық схемасы көрсетілген. Бұдан басқа санды – аналогтық қайта құрулардың ИМС келесі белгілер бойынша классификацияланады:

Шығыс сигналдарының түрі бойынша: тоқтық шығыспен және кернеу түріндегі шығыспен;

Сандық интерфейсінің түрі бойынша: жүйелі енгізумен және кіріс кодының параллельді енгізумен;

Кристаллда ЦАП саны бойынша: бірканалды және көпканалды;

Тез әрекет ету бойынша: жоғарғы және төменгі тез әрекет етулер.