Жиілікті модульдеу 6 страница

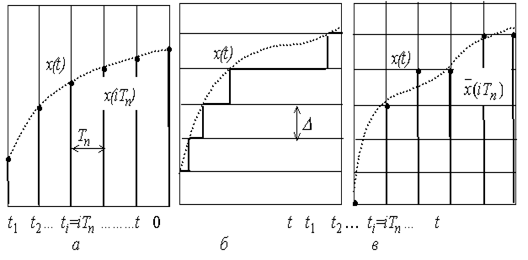
15.2 сур. Сигналдарды уақыт (а); дәреже (б); уақыт және дәреже (в) бойынша кванттау.

Егер дискретті процесстің ақпараттының әрбір кванты уақыт бойынша және импульстердің, оның параметрінің модуляция түрлері көмегімен квантталса, онда дискретті жүйе импульсті деп аталады. Нәтижесінде импульсті жүйенің амплитудалы (АИМ), ұзақтық (ШИМ), фазалық (ФИМ), жиіліктік (ЖИМ) модуляция түрлерін ажыратады. Бұдан басқа аралас түрі бар модуляция жүйелері болады. Егер жүйедегі АИМ импульстер амплитудасы квантталған процесстің белгілеріне пропорциональды болса, онда мұндай импульсті жүйелер сызықтық болады. Модуляцияның басқа да түрлерінде олар сызықтық емес жүйе классына жатады.

Егер САУ дискреттілерде дәреже бойынша квантталған процесстер түрленсе, онда олар релейлы деп аталады. Уақыт және дәреже бойынша квантталған жүйелер сандық деп аталады. Релейлы және сандық жүйелер сызықтық емес болып табылады. Егер сигналдардың барлығы дискретті жүйе болса, онда олар таза дискретті деп аталады, егер сигналдардың бір бөлігі үздіксіз болса, онда олар дискретті үздіксіз деп аталады. Таза дискретті жүйедегі барлық сигналдар және процесстер бірдей дискретті құрлымды болады, онда бұндай жүйе теориясы салыстырмалы жеңіл болады. Дискретті үздіксіз жүйе үздіксіз және таза дискретті арасында аралық жағдай болып табылады, сондықтан оларды зерттеу әдісі қиындау, өйткені үздіксіз және таза дискретті жүйесінің теориялық элементтері қоса болады. Осыдан дискретті жүйесінің теориясын таза дискреттіден бастап зерттеу керек, кейін дискретті үздіксіз жүйелерінің алынған нәтижелерін тарату керек. Терминалогияны қиындатпау үшін «таза дискреттік жүйе» термині қолданылады. Дискретті жүйе теориясының дамуына кеңес одағының ғалымдары Я. 3. Ципкин [16], Л. Т. Кузин [10] және т.б үлес қосқан.

Ары қарай осы тақырыпты қарастырған кезде релейлы жүйе, ҰИМ, ФИМ және ЖИМ импульстік жүйе туралы тұжырымдаймыз. Осы жүйелер туралы мәлімет жоғарыда белгіленген әдебиеттерден алуға болады. Осылайша біз өзіміздің көзқарасымызды сандық және амплитудалы импульсті модуляциясы бар импульстік жүйелерге саламыз. 1.2 сур. көрсетілген кванттау түрлеріне қарасты уақыт және уақыт пен дәреже бойынша квантталған процессті қарастырамыз (. 1.2, а және б сур).

Дискретті жүйедегі процесстердің ерекшелігі

Дискретті жүйедегі ақпараттың түрленуі уақыт немесе уақыт пен дәреже бойынша квантталған дискретті жүйелер түрінде беріледі. Осы процесстерге арнайы белгілер енгізейік. Алғашқы үздіксіз процесстерден шығатын дискреттілерді иілген деп аталады және қарапайым символмен белгіленеді, мысалы x(t).

Уақыт бойынша квантталған және Tn тұрақты кезеңі бар дискретті процесстерге сәйкес процесстерді (1.2, а сур.) x(iTn) арқылы белгілейді, i кез келген толық сан болуы мүмкін. Уақыт және иілгіш бойынша квантталған дискретті процессті алу үшін x(t) функциясына t = iTn белгісін қоюға болады, яғни

x(iTn) = x(t = iTn).

Уақыт бойынша квантталған және Tn тұрақты кезеңі, Δ тұрақты қадамы бар дискретті процессті х(iTn) символымен белгілейміз (1.2, б сур.). Оны берлген иілгіш функция бойынша мына формуламен алуға болады

return false">ссылка скрыта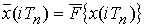

F х(iТn) белгісіне жақын және Δ дәрежесі бойынша квантталған сан операциясы болып табылады. F операциясы сызықты емес болып табылады, сондықтан уақыт және дәреже бойынша квантталған процесстері бар сандық жүйе сызықты емес классқа жатады. Олардың ерекшеліктерін келесіде жеке қарастырамыз, ал қазір уақыт бойынша квантталған х(iТn) процесстері бар сызықты дискретті жүйеге тоқталамыз.

15.3 сур. Дискретті жүйе көрінісі	15.4 сур. Дискретті функцияның бір келкісіздігі

Дискретті жүйенің жұмысы x(iTn) кіріс процесстерінің у(iТn) шығыс процесстеріне кейбір шарттармен түрленуіне негізделген. Схема түрінде ол 1.3 суретінде көрсетілген. Түрлену сипаттамасына байланысты дискретті жүйе үздіксіздер сияқты класстарға бөлінеді, яғни бақылаушы, стабилизациялаушы, интегрирлейтін және т.б, бірақ олардың түрленуі өзіндік ерекшеліктері бар, оларды біз қазір қарастырамыз. x(iTn) дискретті процессінің негізгі ерекшелігі олардың біркелкісіздігі болып табылады. Ол сол дискретті процесске басқа да әр түрлі иілгіштер сәйкес келуімен түсіндіріледі. Мысалы үшін 1.4 суретте екі функция берілген x1(t) және x2(t), оларға х(iТn) процесстері сәйкес келеді. Дискретті функцияның бір келкісіздігі (у(iТn) жүйенің шығыс процессіне қарасты), (1.3 сур.), жүйенің жұмыс нәтижелерінің қате шешімдеріне әкелуі мүмкін, сондықтан пайда болатын бір келіксіздерді минимумға дейін келтіретін шарттарды зерттеу керек. Бір келіксіздердің пайда болуы кванттау кезіндегі уақыт аралығында ақпараттың жоғалуынан болуы мүмкін. Оның қалай болатынын жақсылап қарастырайық. Tn кезеңі және

 

Ω =

2π   Tn

жиілігін кванттаған кезде х(t) = a cos ωt гармониялық процессі де соған тәуелді болады.

Алғашқы процесстің жиілігі мен ω0 иілгіш жиілік арасындағы тәуелділікті табайық (х(iTn) квантталған процесс). Бастапқы жиілік ω << Ω болсын. Квантталған сигнал 1.5, а суретте берілген. x(t) алғашқы процессінің жартылай кезеңінде x(iTn) дискреттік белгілердің үлкен саны қойылады, онда олар арқылы бақылаушыға алғашқы процесстің жиілігімен сәйкес келетін иілгіш жиілігінің белгісін оңай алуға болады. Осылайша онда дискреттік бойынша аздаған жиілігі бар біркелкісіздік болмайды. Егер ω0 тен ω (1.6 сур)тәуелділік құрсақ, онда ол ω << Ω де сызықты болады.

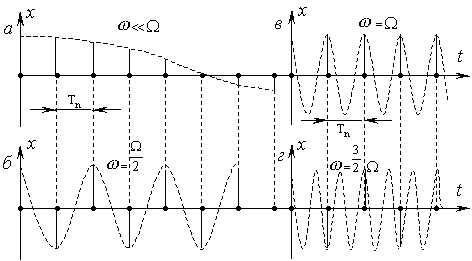
15.5 сур. Гармоникалық сигналды кванттау

15.6 сур. Стробоскопиялық эффект

ω жиілігінің дұрыс бағалануы тек әр бір жартылай кезеңде бір ғана x(iTn) белгі болу керек. Бұл жағдай 1.5, б суретінде көрсетілген және ол мына жиілікке сәйкес келеді

ω =

Ω

ω > да әр бір жартылай кезең x(iTn) бір белгісінен аз келеді, ол ω анықтауда біркелкісіздікке әкеледі. Егер ω = Ω алсақ, онда шығыс процессінің иілгіш жиілігі (1.5, в сур.) ω0 = 0 тең болады, ол 1.6 суретінде берілген.

ω = 3Ω/2 (1.5, г сур) кезінде біз ω = кезіндегі с x(iTn) сәйкес келетін дискретті процессті аламыз (1.5, б сур.). ω жиілігінің бағалануы алғашқы процесстің (ωо дискретті процесстің иілгіш жиілігі бойынша) бір келкісіздігі болады. Бұл тәуелділіктің графигі 1.6 суретінде белгіленген. Біркелкілік тек мына диапазонды сақталады

0 < ω <

Ω

Сипатталған қасиет стробоскопиялық эффект деп аталады және дискретті жүйенің ең қажетті ерекшелігі болып табылады. Осыдан дискретті жүйенің құрауына негізгі шешім қабылданады: дискретті жүйенің еңбекке қабілеттілігі болу үшін және оның шығыс деректері біркелкі интерпретациялы болу керек, сонымен қоса Ω > 2ωгр шартынан кванттау жиілігін таңдау керек, бұл жерде ωгр – кіріс хабардың спектрының максимальды жиілігі. Алғашқы рет оның теоремасын 1933 жылда В. А. Котельников академигі жазған. В. А. Котельников теоремасы Ω кванттау жиілігінің белгісінің минимальділігі немесе Tn дискреттік кезеңінің максимальділігін айқындайды, Tn кезеңі уақыт бойынша квантталатын ақпаратты қатесіз түрлендіреді.

 

Котельников теоремасы, жарықтың жылдамдығының шектеулі сипаттамасы және анықсыздығы шешілмейтін қарама қайшылыққа түседі. Котельников теоремасы «Fв, Гц жиілігінен аспайтын спектор толығымен қалыптасуы мүмкін, егер 1/(2Fв)с уақыт аралығында алынған осы сигналдың есептік белгілері мәлім болса»
Гейзенберг анықсыздық принципі. Микро бөлікшелердің қасиетін тәжірибелік зерттеген кезде (атом, электрон, ядро, фотон т.б) олардың динамикалық өзгерулердің нақтылығы (координат, кинетикалық энергия, импульстер т.б) шектелген және анықсыздық принципімен басқарылады. Осыған сәйкес жүйені ипаттайтын динамикалық өзгерулер екі топқа бөлінеді (қосымша):
1) уақыттық және кеңістік координаттары (t және q);
2) импульс және энергия (p және E).
Осыған орай әр түрлі нақтылық дәрежесінен алынған әр түрлі топтардағы өзгерулерді анықтау мүмкін емес (мысалы, координаттар және импульстер, уақыт және энергия). Бұл жабдықтар мен техника тәжірибе шектеулі шешуші қасиетімен байланысты емес, табиғаттың фундаментальды заңын көрсетеді. Оның математикалық формуласы мына салыстырмалықпен беріледі:
dqdp≈h/2π,(1)
dEdt≈h/2π,(2)
ондағы dq, dp, dE, dt – координат импульс энергия және уақыт өлшемінің анықсыздығы, осыған сәйкес h – тұрақты планка болады.
Эйнштейн постулаты жарық жылдамдығына тұрақты. Салыстырмалық теориясы тұжырымдайды: вакумдағы жарық жылдамдығынан асатын материалды объектілердің ондай жылдамдығы болмайды.
Көбі электрон жылдамдығы жарық жылдамдығына сәйкес бола алмайды деп тұжырымдайды.
Әр жағдайда да нақ осы шақтағы электронның жылдамдығы шектеулі болады.
Материалдық дененің және бөлшектерінің нақ осы шақтағы жылдамдығы шектеулі болу керек, өйткені оның кинетикалық энергиясы шектелген. Күштер мен аймақтардың шектеулі потенциалды энергиясына байланысты бөлшектердің үдеуі – көлемді шектеулік. Траектория – жазық функция, онда барлық уақыт бойынша көлемді өнімдер шектелген (жылдамдық, үдеу, үдеу өзгерісінің темпі т.б).
Яғни кез келген материалдық бөлшектің траекториясы кеңістіктегі шектеулі теңселу спекторымен сипатталады (керек болса уақыт кеңістігінде).
Бұл жағдайда Котельников теоремасына қарасты, бұл шектеулі спекторлы функция спектор шегіне сәйкес келетін жартылай немесе жиіліктің өзі арқылы алынған көлемдік есеп болуы мүмкін. Егер есеп берулер аз ғана қателікпен алынған болса, онда аралық белгілер осындай қателікпен қалпына келуі мүмкін. Бұдан, уақыттағы қателікпен белгіленген бөлшектің (жылдамдық, үдеу) бар екенін білсек онда бұл шкаланың бөлшектенуі өте ұсақ және зеріттелетін көлемнің аралық белгілері осы уақыт функциясындағы шектеулі спектрінен алынады. Осылайша уақытты нақтылау координаттың қателігін ұлғайтуға әкелмейді. Анықсыздық принципі – тәжірибелік жолмен алынған салыстырмалық.
Оның өлшемдерінің нақты көлемі мен нәтижелерін айқындау керек.
Уақыттағы кез келген стационарлы көлемді орталықтандыру оның дисперсиясын төмендетді. Сондықтан кез келген стационарлы көлемді өлшеу нақтылық нәтижесін жоғарлатады (анықталған шекке дейін). Оның керсінше тәуелділігі бар – уақытты өлшеуді қысқарту дисперсия нәтижесін жоғарлатады. Ол өлшемнің аппаратты және әдістемелік қателіктерге байланысты, бірақ өлшемнің қателігінің өсуі дисперсиның ұлғаюына дәлел болмайды. Уақыттың аздаған интервалында біз нашар нақтылықты аламыз. Ол тұрмыстық деңгейде түсінікті – бір нәрсені өлшеу үшін таразы тостағаншалары теңселмеу керек.
Жиілікті өлшеу кезіндегі қателіктерді өлшеу өлшеу интервалының өсуімен төмендейді және оның төмендеуімен өседі. Бұл кейбір жағдайда өлшенетін жиілікте фазалық дивиация сәйкестігі болады. Бірақ, өлшеу интервалын төмендеуімен қателіктердің теориялық өсуі шексіздікке дейін барады, фазалық шулардың өсуі осы тәуелділікке бағынбайды. Осыған орай өлшеу нәтижесінің дисперсия ұзындығы, өлшеу интервалының ұзару белгісінен бастап сигналдың қасиетіне емес өлшеу әдісінің қасиетіне еңгізу керек.
Бұл көріністі зерттеулі бөлшектерге және басқада өлшеулерге қолданады. Нәтиже девиациясының өсуін тәжірибелік бақылаған да өлшеу құрылғы қателігінің (бақылаушы) жабдықтар өлшегішінің қасиетін анықтайды, бірақ нақ осы шақтағы бөлшектер траекториясына ешқандай қатысы жоқ. Теорияда өзіндік траектрия түріне орын жоқ. Элементарлы бөлшектердің теориялық механикасында негізгі шарттар мен зандылықтардың терминдерінде алғашқы тапсырма шарттары түрленеді, ондағы шешімдер мүмкін белгілерде түрлендеу керек, керсінше алғашқы шарттағы нақты нәтижесінен алынған нақты басқару түрінде болу керек.
Егер алғашқы шарттар белгілі болса (өлшеу нәтижесінде), онда траекториялар сәйкес анықсыздықпен өлшенген және есептелген болу керек.
Басқаша айтқанда, зеріттеулі тапсырма анықсыздық прнципіне бағыну керек, яғни белгілі қателік алдынғы және келесі көлемдік есептермен сәйкестікке арналған теориялық есеппен кемуі тиіс емес. Бірақта, Котельников теоремас мен алынған нәтижесінен аспау керек.
Теориялық тапсырма (алғашқы заттардың нақты білімін принципке жіберетін) оған бағынбау керек, яғни жіберілген азғантай қателіктердегі алғашқы параметрлердің көрсетілуі статистикалық және детерминирленген есепті беру керек.
Мысалы, классикалық түрдегі теориялық механикадағы денелердің кедергі күштерінің болмауында дене өзінің тепетеңдігін және қозғалыстың түзу сызықтылығын көпке дейін сақтауы мүмкін. Тәжірибе жүзінде, мұз қанша тайғанақ болса да шайба әрқашан тоқтайды. Нөлдік үйкелісу қамтамасыз ету мүмкін емес.
Бірақ өлшеу әдісінің анықсыздық нәтижесі ретінде қарастыруға болады. Мысалы, t1 интервалында элементарлы бөлшекте x1 координатасы бар делік, импульс p1, энергия E1 және бұл өлшемдер қателіктен болған делік, осыған сәйкес dt, dx, dp, dE. Сонда, t2=t1/N интервалын таңдаған кезде (t1 интервалының ішінде), N белгісі (2) салыстырмалықты сақтайды.Осыған орай t2 нөлге тырмысады. Бұл үшін ((2) салыстырмалығы орындалуды жалғастыру үшін) dE шексіздікке дейін өсуін қамтамасыз ету керек. Әрине ондай ешқашан болмайды, кез келген бөлшектің соңғы энергиясы болады.
Осыған сәйкес кез келген траекторияда электрон өзінің энергиясын жоғартты делік (мысалы, екі есе) онда егер кішкене қателік болсада осы екі белгі арасында электронның осы траекторияның аралық нүктесінде орталық мағынасы болды. Біз осы орта белгіні бірнеше рет қолдануымызғ болады. Әрине бір мезетте электрон осы белгіге ие болғанү. Біз теориялық тұрғыдан нөлдік қателігі бар энергияны атауға болады. Ол үшін (1) салыстырмалық орындалу үшін берілген траекториядан электронның қалысуының шексіздікке дейін өсуі керек. Қызық көрініс: тіркелген электрон, Қарағанды лабораториясында қолданылатын, кішкене интервалда кішкене қалысу керек , сол кезде ол Алматыға дейін ұшуы керек. Одан аз интервалда ол тіпті айға дейін, одан азында күнге дейін, оданда азында сириусқа дейін ұшу керек.
Онда бұл энергия үздіксіз үлкендік емес, дискретті. Онда логикалық тұжырымдағанда біз кеңістікте дискретті көлемдерден тұратынын, уақыттың үздіксіз емес өтуін, яғни дискретті, табиғаттағ барлық көрініс дискретті жағдайдың жалғасуы деп дәлелдеуімізге болушы еді.
Осындай көріністің екі кемшілігі бар, аникалық схоласт Зенон бұл ойды бірнешерет тұжырымдаған, бірақ ғылым оны бірнеше рет шектеткен.
1. Егер дискретті көлемдік оның үлкен кемшілігіне қарасты өлшенбейді, онда оның дискреттілігі туралы айту да қажет жоқ, жай айтқанда үздіксіз көлемдік туралы айтқан ыңғайлы. Сфера түзу қиындылармен сәйкестелген көрінісін айқындауға болады, бірақ осы қиындылардың ұзындықтары шексіз азаюында (оның бір мезетте ұлғаюы) басқа көрініс береді – көп бұрыш сфераға абстракцияның шектелген белгі ретінде ауысады. Егер біз қозғалысты тұрақты жылдамдықты қозғалыстардың кезектесіп ауысуын елестетсек онда біз интервалдар шектерінде шексіз үдеуді анықтай аламыз.

2. Егер дискретті көлем өзіндік алынған болса онда дискрет туралы емес жылжымалы функция туралы айтамыз. Атомдар, иондар және молекулалар сәулелену спекторы энергиясы – бұл жылжымалы түрде ауыспалы функция. Спектрлерді Доплерлік кеңейткенде және басқада әйгілі көріністердің орны болмаушы еді, егер энергия барлық әсерлесу жағдайлары үшін фиксерленген дискретті түрде өзгерсе. Бірақ квант энергиясы – бұл ауыспалы көлем (ұлғаю). Осылайша энергияның дискреттілігі туралы айту мүмкін емес.

 

Тақырып 9. Жіберу процесстерінің моделі.

Мақсаты: үздіксіз және дискретті байланыс каналдардың негізгі моделін қарастыру.

Жоспар (1 сағат)

1.Ақпаратты өлшеу.

2.Үздіксіз және дискретті байланыс каналдарының моделі.

3.Үздіксіз және дискретті байланыс каналдарының өткізу мүмкіндіктері. .

Кілттік сөздер:канал, байланыс, сигнал, ақпарат, жіберу, мүмкіндік, модель, процесс.

Ақпараттың сигнал қуаттылығы ақпаратты тасымалдау салмағы сияқты ақпараттың көлемін бағалай алмайды.
• Ескі кітап, егер ондағы беттер толық болса ол сізге жаңа кітап сияқты соншалықты ақпарат береді.
• Тасты скрижаль, салмағы үш тонна, археологиялық журналдағы жақсы сурет сияқты археологтарға соншалықты ақпарат береді.
• Радио студия соңғы жаңалықтарды берген кезде мәскеулік тұрғын, Қарағанды тұрғыны бірдей ақпарат алады, бірақ Қарағандыдағы радиотолқынның энергия ағымы Алматыныкінен аздау.
1. Тұрмыстағы ақпаратты өлшеу (ақпараттың жаңа түрі).
Сіз қандайда бір хабар алдыңыз (мысалы, өзіңіз жақсы көретін журналдан мақаланы оқыдыңыз). Бұл мақалада қандайда бір ақпарат көлемі бар. Қалай бағалауға болады, қанша ақпарат алдыңыз? Басқаша айтқанда, ақпарат қалай өлшенеді? Мақала қанша үлкен болса сонша ақпарат бар деп айтуға болады ма?
Бірдей хабар алған әр түрлі адамдар ақпараттың көлемін өздерінше әр түрлі бағалайды. Бұның бәрі адамдардың білімділік деңгейі осы хабар алғанға дейін әр түрлі болды. Сондықтан бұл хабар туралы аз білген адамдар көп ақпарат алды деп ойлайды, ал кім көп білді олар ақпаратты мүлдем алмаған сияқты болады. Хабардағы ақпараттың көлемі тұтынушының осы хабарға деген қажеттілігіне байланысты.
Осылай тұжырымдасақ ақпаратты өлшеу бірліктерін қандай критерилар арқылы еңгізуге болатыны түсініксіз. Ақпараттың көзқарасы бойынша біз ақпараттың ғылыми ашылуларда, әуендік стильде қоғамдық дамудың жаңа теорияларындағы көлемді бағалай аламыз.
2. Техникадағы ақпаратты өлшеу.
Техникадағы (хабарды тасымалдау және кодтау теориясы) ақпарат көлемін символдардың кодталатын мөлшері, тасымалдануы немесе сақталуы ретінде түсінеді.
Техникада (белгілер мен символдардың тасымалдануы, өңделуі, сақталуы ақпарат деп есептеледі) көбінесе ақпарат көлемін анықтаудың оңай тәсілін қолданады, ол ақпарат көлемді деп аталынуы мүмкін. Ол хабардағы символдар санының есептеуіне негізделген, яғни ұзындықпен байланысты және мазмұнды есепке алмайды.
Есептеуіш техникада екі стандартты өлшем бірліктері қолданылады: бит (binary digit) және байт (byte).
Бит – екілік алфавиттің екілік белгісі {0, 1}.

Бит – ақпаратты өлшеудің минимальды бірлігі.
Байт – СИ жүйесіндегі ақпарат көлемінің бірлігі.

Байт – сегізразрядты екілік код, оның көмегімен бір символды көруге болады.в

Клавиатурадан белгілерді ЭЕМ ге еңгізгенде машинаға бір байт ақпарат беріледі.
Есептеуіш техникадағы ақпаратты өлшеу бірдігі бит, ал ақпараттың элементарлы бірлігі байт8бит
килобайт210байт=1024байт
мегабайт210Кбайт=220байт
гигабайт210Мбайт=230байт
Хабардың ақпараттық көлемі (хабардың ақпараттық өлшемі) - бит, байт немесе өңделген бірліктермен (Кбайтах, Мбайтах және т.б) өлшенген ақпарат көлемі. Хабардың ұзындығы хабарды жазуға пайдаланатын әр түрлі символдардың санына байланысты.
Мысалы, "мир" деген сөз орысша алфавитте үш белгімен беріледі, ал ағылшынша тілде бес (реасе), ал КОИ-8 де жиырма төрт биттермен беріледі (111011011110100111110010).
Алғашқы хабар тілдің ақпараттық көлемінің машиналық тілмен көрінуі (КОИ-8) символдар, биттер және байттарда
Рим 11110010 11101001 11101101 3 24 3
мир 11101101 11101001 11110010 3 24 3
миру мир! 11101101 11101001 11110010
11110101 00100000 11101101
11101001 11110010 00100001 9 72 9
Егер сіз РИМ деген сөзде жиырма төрт битті ақпарат бар, ал МИРУ МИР! деген сөзде жетпіс екі бит бар деп айтсаңыз дұрыс болады. Бірақ, битпен ақпаратты өлшеу алдында сіз осы хабардағы символдар мөлшерін анықтауыңыз керек. Бізге символдармен, ал машинаға кодтармен жұмыс істеу үйреншікті. Әр бір символ сегіз битті кодпен жайдан жай кодталынбайды. Сондықтан ыңғайлылық үшін техникаға ақпараттың «үлкен» бірлігі жаңадан еңгізілді – байт. Енді сізге техникалық хабарламадағы ақпараттың көлемін жеңіл есептеуіңізге болады – ондағы символдар көлемімен сәйкес келеді.
3. Ақпарат теориясындағы ақпаратты өлшеу (ақпарат түсірілмеген анықталмағандық сияқты).
Ақпарат теориясында ақпарат көлемін оның формасына, мазмұнына және анықсыздыққа (берілген сигнал түрінде берілген хабарды алғаннан кейін жоғаады) сигналдың сандық сипаттамасы, бұл жағдайда ақпараттың көлемі хабарды сол немесе басқа оқиғадан алынуына тәуелді.
Абсолютті сенімді оқиға үшін (оқиға міндетті түрде болады, сондықтан болу мүмкіндігі бірге тең) хабардағы мүмкіндік көлемі ол туралы О тең. Оқиға қаншалықты мүмкін болса, хабардағы ақпарат соншалықты көп болады.
Тек мүмкіндікке жақын жауаптар ИӘ немесе ЖОҚдеген сөздер бір бит ақпарат береді. Ақпарат көлемін бағалау ақпарат теориясының заңына негізделеді. Хабар бағалы тек егер бізге хабардың мағынасы түсінікті болса.

Ақпаратты беру арналары тағайындалуы бойынша телефондық, телеметрикалық, сандық мәліметтерді беру сияқт

Ақпаратты беру арналары тағайындалуы бойынша телефондық, телеметрикалық, сандық мәліметтерді беру сияқты негізгі түрлергі жіктеледі. Байланыс желілерінің сипатына байланысты радиобайланыс және проводты байланыс арналары болады: кабельдік, толқынды, волоконды-оптикалық және т.б. Жүздеген килогерцтен ондаған мегагерцке дейін диапазонда жұмыс істейтін кабельді байланыс арналары ең жақсы қасиеттерге ие.