Алфавит Х из р символов и правила записи (изображения) и обработки чисел с помощью символов этого алфавита называются системой счисления (нумерацией) с основанием р. Число х в системе с основанием р обозначается как (х)р или хр .
Любая система счисления – это система кодирования числовых величин (количеств), позволяющая выполнять операции кодирования и декодирования, то есть по любой количественной величине однозначно находить его кодовое представление и по любой кодовой записи – восстанавливать соответствующую ей числовую величину.
Все системы счисления строятся по общему принципу: определяется величина р – основание системы, а любое число х записывается в виде комбинации степеней веса р от 0-й до n-й степени следующим образом:
(x)10 = xnpn + xn–1pn–1 + ... + x1p1 + x0p0 .
Наиболее используемые в информатике системы счисления, кроме, естественно, десятичной, – это: 1) двоичная, над алфавитом Х = {0,1}; 2) восьмеричная, над Х = {0, 1, 2, 3, 4, 5, 6, 7}; 3) шестнадцатеричная, над Х = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, Е, F}, где символы А, В, С, D, Е, F имеют, соответственно, десятичные веса 10, 11, 12, 13, 14, 15.
Пример. 11012 = 1 x 23 + 1 x 22 + 0 x 21 + 1 x 20 = 8 + 4 + 1 = 1310 ,
1578 = 1 x 82 + 5 x 81 + 7 x 80 = 64 + 40 + 7 = 11110 ,
A6F16 = 10 x 256 + 6 x 16 + 15 x 1 = 267110 .
В большинстве систем счисления вес цифры (или символа алфавита) зависит от ее места в записи числа или слова. Такая система счисления называется позиционной ; в противном случае система называется непозиционной .
Пример. Непозиционная система – древняя римская система записи чисел с алфавитом вида Х={I (1), V (5), Х (10), L (50), С (100), D (500), М (1000)}, где в скобках указаны веса символов (не зависящие от позиции символа). Примеры римских чисел (в скобках – обычные десятичные эквиваленты): III (3), IV (4), V (5), VI (6), IX (9), XI (11), DCL (650). Запись числа в этой системе получается двусторонней конкатенацией, причем правая конкатенация ассоциируется с добавлением, а левая конкатенация – с убавлением (например, IV и VI). Поразрядное же выполнение арифметических операций не имеет места (например, XIV + IV  XVIII ).
Для изображения десятичных дробей используется подобная формула разложения по степеням основания.
Пример. 110,0012 = 1x22 + 1 x 21 + 0 x 20 + 0 x 2-1 + 0 x 2-2 + 1 x 2-3 = 6,12510 ;
A,B16 = A x 160 + B x 16-1 = 10 x 1 + 11 x 0,0625 = 10,687510 .
Процедура перевода десятичных чисел в р-ную систему счисления:
1. перевести отдельно целую часть числа х, для чего последовательно делить сперва целую часть [х]10 , а затем все частные (получаемые при делении) на р до тех пор, пока не получим в очередном частном число меньшее р; изображение [х]p получается последовательным приписыванием к последнему частному остатков от деления – от последнего до первого;
2. перевести отдельно дробную часть (мантиссу) числа, то есть {x}10 , для чего последовательно умножать сперва исходную мантиссу, а затем мантиссы получаемых чисел на р до тех пор, пока не получим мантиссу, равную нулю, или нужное количество цифр в {х}p ; изображение {х}p получается приписыванием к целой части первого произведения второй такой же цифры и т.д., до последней цифры целой части;
3. результат будет иметь вид (х)р = [х]p, {х}p .
Пример. Найти: 12,810 = ?2 . Решение:
1. Переводим целую часть: 1210 =11002;
2. переводим дробную часть: 0,8 x 2 = 1,6; 0,6 x 2 = 1,2; 0,2 x 2 = 0,4; 0,4 x 2 = 0,8; 0,810 = 0,1100110...2 ;
3. результат перевода: 12,810 = 1100,1100110011...2 .
Пример. Найдем 29,2510 = ?8 . Решение имеет вид 1) 2910 = 358 ; 2) 0,2510 = 0,28 ; 3) 29,2510 = 35,28 .
Пример. Найдем 79,2610 = ?16 . Решение: 1) 7910 = 4F16 ; 2) 0,2610 = 0,4016 ; 3) 79,2610 = 4F,416 . При переводе дробной части мы ограничились нахождением двух значащих цифр после запятой, ибо перевод точно сделать невозможно.
Для перевода из 2-ной в 8-ную и наоборот, из 2-ной в 16-ную и наоборот, из 8-ной в 16-ную и обратно, используется таблица следующего вида: XVIII ).
Для изображения десятичных дробей используется подобная формула разложения по степеням основания.
Пример. 110,0012 = 1x22 + 1 x 21 + 0 x 20 + 0 x 2-1 + 0 x 2-2 + 1 x 2-3 = 6,12510 ;
A,B16 = A x 160 + B x 16-1 = 10 x 1 + 11 x 0,0625 = 10,687510 .
Процедура перевода десятичных чисел в р-ную систему счисления:
1. перевести отдельно целую часть числа х, для чего последовательно делить сперва целую часть [х]10 , а затем все частные (получаемые при делении) на р до тех пор, пока не получим в очередном частном число меньшее р; изображение [х]p получается последовательным приписыванием к последнему частному остатков от деления – от последнего до первого;
2. перевести отдельно дробную часть (мантиссу) числа, то есть {x}10 , для чего последовательно умножать сперва исходную мантиссу, а затем мантиссы получаемых чисел на р до тех пор, пока не получим мантиссу, равную нулю, или нужное количество цифр в {х}p ; изображение {х}p получается приписыванием к целой части первого произведения второй такой же цифры и т.д., до последней цифры целой части;
3. результат будет иметь вид (х)р = [х]p, {х}p .
Пример. Найти: 12,810 = ?2 . Решение:
1. Переводим целую часть: 1210 =11002;
2. переводим дробную часть: 0,8 x 2 = 1,6; 0,6 x 2 = 1,2; 0,2 x 2 = 0,4; 0,4 x 2 = 0,8; 0,810 = 0,1100110...2 ;
3. результат перевода: 12,810 = 1100,1100110011...2 .
Пример. Найдем 29,2510 = ?8 . Решение имеет вид 1) 2910 = 358 ; 2) 0,2510 = 0,28 ; 3) 29,2510 = 35,28 .
Пример. Найдем 79,2610 = ?16 . Решение: 1) 7910 = 4F16 ; 2) 0,2610 = 0,4016 ; 3) 79,2610 = 4F,416 . При переводе дробной части мы ограничились нахождением двух значащих цифр после запятой, ибо перевод точно сделать невозможно.
Для перевода из 2-ной в 8-ную и наоборот, из 2-ной в 16-ную и наоборот, из 8-ной в 16-ную и обратно, используется таблица следующего вида:
| ОСНОВАНИЕ СИСТЕМЫ
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
| —
|
|
| |
| —
|
|
| |
| —
|
|
| |
| —
|
|
| |
| —
|
|
| |
| —
|
|
| |
| —
| —
|
| |
| —
| —
|
| |
| —
| —
|
| |
| —
| —
|
| |
| —
| —
|
| |
| —
| —
|
| |
| —
| —
|
| |
| —
| —
|
| При переводе в 8-ную систему или из нее необходимо группировать в тройки биты, а при переводе в 16-ную или из нее – группировать их в четверки битов. Можно добавлять, если нужно, незначащие нули (слева от целой части и справа от мантиссы) или отбрасывать их.
Пример. Рассмотрим переводы в смешанных системах.
1. Из 2-ной системы в 8-ную (двоично-восьмеричное изображение):

2. из 8-ной системы в 2–ную (восьмерично-двоичное изображение):

3. из 2-ной системы в 16-ную (двоично-шестнадцатеричное изображение):

4. из 16-ной системы в 2-ную (шестнадцатерично-двоичное изображение):

Сложение в двоичной системе счисления осуществляется по правилам
0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, 1 + 1 = 210 = 102 (единица идет в старший разряд).
Таблица вычитания в двоичной системе счисления имеет вид
0 – 0 = 0, 1 – 0 = 1, 1 – 1 = 0, 0 – 1 = 10 – 1 = 1 (единицу забираем у старшего разряда).
Таблица умножения в двоичной системе счисления имеет вид
0 x 0 = 0, 0 x 1 = 0, 1 x 0 = 0, 1 x 1 = 1.
Таблица деления в двоичной системе счисления имеет вид
0 : 0 = не определено, 1 : 0 = не определено, 0 : 1 = 0, 1 : 1 = 1.
Обратным кодом числа в системе с основанием р называется число в этой системе, получаемое заменой цифры, символа в каждом разряде числа на его дополнение до максимальной цифры в системе (то есть до р – 1).
Дополнительный код = обратный код + единица в младшем разряде.
Пример.
1. 10011  двоичное число, двоичное число,
01100  обратный код этого двоичного числа, обратный код этого двоичного числа,
01101  дополнительный код этого двоичного числа; дополнительный код этого двоичного числа;
2. 457  восьмеричное число, восьмеричное число,
321  дополнительный код; дополнительный код;
3. А9  шестнадцатеричное число, шестнадцатеричное число,
57  дополнительный код. дополнительный код.
Вычитание с помощью дополнительного кода: найти дополнительный код вычитаемого такой же разрядности, как и уменьшаемое, и сложить этот код с уменьшаемым. Результатом вычитания будет полученная сумма без учета старшего разряда (отбрасывается).
Пример. Выполним вычитание напрямую и через сложение (через дополнительный код):

Целые числа в математике и их аналоги в n-разрядных арифметиках тождественны (по количеству) в рамках их представления с этой разрядностью. При этом можно отметить основные отличия представления чисел в поле памяти человека и в поле памяти n-разрядной арифметики:
1. бесконечное и счетное множество целых чисел представляется отрезком [–N; +N], где N – максимальное число, представимое в этой арифметике (многоточие – общее число единиц, равное n): N = (111 . . . 1)2 ;
2. бесконечное и несчетное множество действительных чисел  , располагающееся на числовой оси равномерно и плотно, представляется в n-разрядной арифметике множеством с неравномерной плотностью (сгущение у нуля и сжатость со стороны меньших чисел); , располагающееся на числовой оси равномерно и плотно, представляется в n-разрядной арифметике множеством с неравномерной плотностью (сгущение у нуля и сжатость со стороны меньших чисел);
3. нуль во множестве действительных чисел в любой своей окрестности имеет множество чисел, а нуль в n-разрядной арифметике представлен изолированно.
С точки зрения обычной арифметики, например, в интервале (–1; 1) имеется бесконечное множество "плотно" расположенных точек, причем в любой окрестности каждой такой точки имеется хотя бы одна точка из этого множества. Такую арифметику называют часто регулярной арифметикой. Машинная же арифметика имеет следующие особенности. Она нерегулярна – точки интервала сгущаются около нуля; кроме того, в этом интервале точка х "изолирована" – если взять любую ее окрестность (х – а; х + а), где а – число, которое не превосходит машинного нуля (наименьшего представимого в машине числа), то в этом интервале нет других точек (отличных от х). Говоря языком теории вероятности, плотности распределения чисел в регулярной и нерегулярной арифметике – различны, как, впрочем, плотности распределения целых и вещественных чисел в одной и той же арифметике. Множество вещественных чисел в машинной арифметике представляется как подмножество (определяемое разрядностью арифметики) множества рациональных чисел. Есть и другие особенности этих множеств (связанные, например, с выполнением операций), но указанные выше особенности – основные.
Различия в представлении чисел в обычной и в машинной (n-разрядной) арифметике ограничивают как "математические" возможности компьютера, так и "компьютерные" возможности математики, использование математических методов, алгоритмов в компьютерах.
Нужно всегда иметь в виду, что точность в теоретической математике – понятие абстрактное и в практической математике может возникать иллюзия точности там, где ее на самом деле нет, – если нет корректной договоренности о пределах возможных значений неизбежных погрешностей в рамках рассматриваемых вычислительных ресурсов, например, трудоемкости и времени, а также не оговорена стратегия управления этой погрешностью.
Так как диапазон n-разрядных чисел системы счисления с основанием p находится в пределах  , то для представления дробных чисел этот диапазон еще снижается, поскольку часть разрядов необходимо отвести под изображение мантиссы. Таким образом, имеются так называемые "зоны нечувствительности" форм представления чисел в n-разрядных арифметиках. , то для представления дробных чисел этот диапазон еще снижается, поскольку часть разрядов необходимо отвести под изображение мантиссы. Таким образом, имеются так называемые "зоны нечувствительности" форм представления чисел в n-разрядных арифметиках.
В 1937 году Конрадом Цузе для увеличения диапазона чисел, представимых в арифметике двоичных чисел, а также для повышения точности этого представления чисел было предложено представление чисел в плавающей, нормализованной форме – число x представляется в виде:  , где m – мантисса числа, k – целый порядок числа, , где m – мантисса числа, k – целый порядок числа,  . .
Пусть даны два числа:  и и  ( ( ). Тогда можно проверить, что результаты выполнения операций будут равны: ). Тогда можно проверить, что результаты выполнения операций будут равны:

Если из n разрядов, отводимых под изображение чисел, m двоичных разрядов отвести под мантиссу, k – под порядок, один разряд – под знак числа и один разряд – под знак порядка (например, 0 – плюс, 1 – минус), то диапазон представимых в форме с плавающей запятой чисел резко увеличивается (m + k + 2 = n):

(многоточие соответствует k единицам).
Числа, меньшие нижней границы положительных чисел и большие верхней границы отрицательных чисел, считаются равными нулю, не различаются между собой. Числа, большие верхней границы положительных чисел, полагаются равными положительной бесконечности (меньшие нижней границы отрицательных – отрицательной бесконечности). Сравнение двух разных по величине чисел в арифметике с ограниченной разрядностью может поэтому приводить к неверному результату, как и сравнение двух равных в таких системах чисел с точки зрения математической.
Такое представление очень удобно для хранения в ЭВМ, так как на самом деле необходимо хранить не само число, а его знак, мантиссу, порядок и знак порядка, и все операции с числами сводятся к операциям с этими объектами. Операции же с этими объектами просты: сравнение знаков, увеличение, уменьшение порядка, сложение мантисс, нормализация, то есть в конечном итоге сводятся к достаточно просто реализуемым операциям сдвига, выравнивания, сравнения разрядов.
Пример. Вычислить наибольшее и наименьшее 5-разрядное целое число в системе счисления с основанием 3. Наибольшее целое n-разрядное число, которое возможно записать в системе счисления с основанием р, равно:

Наименьшее целое n-разрядное число в этой системе равно

Таким образом, в системе счисления с основанием 3 и числом разрядов 5 представим диапазон следующих чисел:

Формулам можно придать более компактный вид. Например, для двоичной системы

а в восьмеричной системе счисления эти числа
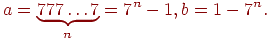
К "неудобствам" этой формы представления чисел можно отнести возможность возникновения следующих "особо опасных" ситуаций:
1. если число достаточно мало, например, а = 0.12Е + 00, то оно может быть представлено любым числом из наименьшего интервала включающего а, в частности числом 0.120000001 или 0.199999999 и в этом случае сравнивать на равенство "в лоб" нельзя (вещественные числа в форме с плавающей запятой опасно сравнивать на совпадение);
2. порядок выполнения операций может влиять на результат, например, в 4-разрядной арифметике с фиксированной запятой 20.0000 + 0.0001 = 20.0001, но при этом 0.2000Е + 02 + 0.1000Е – 05 = 0.2000Е + 02;
3. может возникнуть так называемая ситуация "переполнения порядка" при сложении (умножении) очень больших чисел или "исчезновения порядка" при сложении (умножении) "очень малых чисел", в частности, 0.6000Е + 39 ×0.1200Е + 64 = 0.9999Е + 99 (или же не определено), а также 0.6000Е – 35 × 0.0200Е – 65 = 0.9999Е – 99 (или же не определено), при соответствующим образом определенной разрядности десятичной арифметики;
4. при сложении чисел с плавающей запятой (а, в конечном счете, все операции выполняются через сложение) происходит выравнивание порядков для последующего сложения мантисс, а при выравнивании степеней может происходить потеря (усечение) младших разрядов, например, такая ситуация может возникнуть при сложении одного "очень большого числа" с одним "очень малым числом"
Есть много различных способов (часто искусственных) формирования систем чисел.
Пример. В факториальной системе счисления целые числа записывают линейной комбинацией факториалов, например,  . Эта система (условно) позиционна. Так как 0! = 1! = 1, то два младших разряда n-разрядного числа . Эта система (условно) позиционна. Так как 0! = 1! = 1, то два младших разряда n-разрядного числа  в разложении этого числа по факториалам представимы как в разложении этого числа по факториалам представимы как 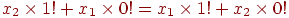 и поэтому веса этих разрядов не зависят от позиции (поэтому при и поэтому веса этих разрядов не зависят от позиции (поэтому при  это число можно считать непозиционным лишь условно). Формула перевода из факториальной системы счисления в десятичную систему: это число можно считать непозиционным лишь условно). Формула перевода из факториальной системы счисления в десятичную систему:

История развития систем счисления достаточно интересна. Приведем лишь некоторые факты. Счет вначале велся с помощью пальцев рук (пятерками и затем – десятками). В некоторых странах сохранился счет с основанием 12 (например, Великобритания – 12 шиллингов) и 20 (например, Франция – "quatre–vingts" или "четыре-двадцать" то есть 80; у древних адыгов счет велся аналогично: "тощIищ", то есть "двадцать-три" – 60) и др.
|
 XVIII ).
Для изображения десятичных дробей используется подобная формула разложения по степеням основания.
Пример. 110,0012 = 1x22 + 1 x 21 + 0 x 20 + 0 x 2-1 + 0 x 2-2 + 1 x 2-3 = 6,12510 ;
A,B16 = A x 160 + B x 16-1 = 10 x 1 + 11 x 0,0625 = 10,687510 .
Процедура перевода десятичных чисел в р-ную систему счисления:
1. перевести отдельно целую часть числа х, для чего последовательно делить сперва целую часть [х]10 , а затем все частные (получаемые при делении) на р до тех пор, пока не получим в очередном частном число меньшее р; изображение [х]p получается последовательным приписыванием к последнему частному остатков от деления – от последнего до первого;
2. перевести отдельно дробную часть (мантиссу) числа, то есть {x}10 , для чего последовательно умножать сперва исходную мантиссу, а затем мантиссы получаемых чисел на р до тех пор, пока не получим мантиссу, равную нулю, или нужное количество цифр в {х}p ; изображение {х}p получается приписыванием к целой части первого произведения второй такой же цифры и т.д., до последней цифры целой части;
3. результат будет иметь вид (х)р = [х]p, {х}p .
Пример. Найти: 12,810 = ?2 . Решение:
1. Переводим целую часть: 1210 =11002;
2. переводим дробную часть: 0,8 x 2 = 1,6; 0,6 x 2 = 1,2; 0,2 x 2 = 0,4; 0,4 x 2 = 0,8; 0,810 = 0,1100110...2 ;
3. результат перевода: 12,810 = 1100,1100110011...2 .
Пример. Найдем 29,2510 = ?8 . Решение имеет вид 1) 2910 = 358 ; 2) 0,2510 = 0,28 ; 3) 29,2510 = 35,28 .
Пример. Найдем 79,2610 = ?16 . Решение: 1) 7910 = 4F16 ; 2) 0,2610 = 0,4016 ; 3) 79,2610 = 4F,416 . При переводе дробной части мы ограничились нахождением двух значащих цифр после запятой, ибо перевод точно сделать невозможно.
Для перевода из 2-ной в 8-ную и наоборот, из 2-ной в 16-ную и наоборот, из 8-ной в 16-ную и обратно, используется таблица следующего вида:
XVIII ).
Для изображения десятичных дробей используется подобная формула разложения по степеням основания.
Пример. 110,0012 = 1x22 + 1 x 21 + 0 x 20 + 0 x 2-1 + 0 x 2-2 + 1 x 2-3 = 6,12510 ;
A,B16 = A x 160 + B x 16-1 = 10 x 1 + 11 x 0,0625 = 10,687510 .
Процедура перевода десятичных чисел в р-ную систему счисления:
1. перевести отдельно целую часть числа х, для чего последовательно делить сперва целую часть [х]10 , а затем все частные (получаемые при делении) на р до тех пор, пока не получим в очередном частном число меньшее р; изображение [х]p получается последовательным приписыванием к последнему частному остатков от деления – от последнего до первого;
2. перевести отдельно дробную часть (мантиссу) числа, то есть {x}10 , для чего последовательно умножать сперва исходную мантиссу, а затем мантиссы получаемых чисел на р до тех пор, пока не получим мантиссу, равную нулю, или нужное количество цифр в {х}p ; изображение {х}p получается приписыванием к целой части первого произведения второй такой же цифры и т.д., до последней цифры целой части;
3. результат будет иметь вид (х)р = [х]p, {х}p .
Пример. Найти: 12,810 = ?2 . Решение:
1. Переводим целую часть: 1210 =11002;
2. переводим дробную часть: 0,8 x 2 = 1,6; 0,6 x 2 = 1,2; 0,2 x 2 = 0,4; 0,4 x 2 = 0,8; 0,810 = 0,1100110...2 ;
3. результат перевода: 12,810 = 1100,1100110011...2 .
Пример. Найдем 29,2510 = ?8 . Решение имеет вид 1) 2910 = 358 ; 2) 0,2510 = 0,28 ; 3) 29,2510 = 35,28 .
Пример. Найдем 79,2610 = ?16 . Решение: 1) 7910 = 4F16 ; 2) 0,2610 = 0,4016 ; 3) 79,2610 = 4F,416 . При переводе дробной части мы ограничились нахождением двух значащих цифр после запятой, ибо перевод точно сделать невозможно.
Для перевода из 2-ной в 8-ную и наоборот, из 2-ной в 16-ную и наоборот, из 8-ной в 16-ную и обратно, используется таблица следующего вида:




 двоичное число,
двоичное число,
 , располагающееся на числовой оси равномерно и плотно, представляется в n-разрядной арифметике множеством с неравномерной плотностью (сгущение у нуля и сжатость со стороны меньших чисел);
, располагающееся на числовой оси равномерно и плотно, представляется в n-разрядной арифметике множеством с неравномерной плотностью (сгущение у нуля и сжатость со стороны меньших чисел); , то для представления дробных чисел этот диапазон еще снижается, поскольку часть разрядов необходимо отвести под изображение мантиссы. Таким образом, имеются так называемые "зоны нечувствительности" форм представления чисел в n-разрядных арифметиках.
, то для представления дробных чисел этот диапазон еще снижается, поскольку часть разрядов необходимо отвести под изображение мантиссы. Таким образом, имеются так называемые "зоны нечувствительности" форм представления чисел в n-разрядных арифметиках. , где m – мантисса числа, k – целый порядок числа,
, где m – мантисса числа, k – целый порядок числа,  .
. (
( ). Тогда можно проверить, что результаты выполнения операций будут равны:
). Тогда можно проверить, что результаты выполнения операций будут равны:





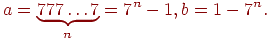
 . Эта система (условно) позиционна. Так как 0! = 1! = 1, то два младших разряда n-разрядного числа
. Эта система (условно) позиционна. Так как 0! = 1! = 1, то два младших разряда n-разрядного числа  в разложении этого числа по факториалам представимы как
в разложении этого числа по факториалам представимы как 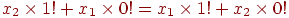 и поэтому веса этих разрядов не зависят от позиции (поэтому при
и поэтому веса этих разрядов не зависят от позиции (поэтому при  это число можно считать непозиционным лишь условно). Формула перевода из факториальной системы счисления в десятичную систему:
это число можно считать непозиционным лишь условно). Формула перевода из факториальной системы счисления в десятичную систему:

 Получаем, что
Получаем, что  .
Множество логических переменных
.
Множество логических переменных  – логического сложения или дизъюнкции ,
– логического сложения или дизъюнкции ,  – логического умножения или конъюнкции называется алгеброй предикатов (и высказываний) , если эти операции удовлетворяют следующим аксиомам:
1. Аксиома двойного отрицания:
– логического умножения или конъюнкции называется алгеброй предикатов (и высказываний) , если эти операции удовлетворяют следующим аксиомам:
1. Аксиома двойного отрицания:
 2. Аксиомы переместительности операндов (относительно операций дизъюнкции и конъюнкции):
2. Аксиомы переместительности операндов (относительно операций дизъюнкции и конъюнкции):
 3. Аксиомы переместительности операций дизъюнкции и конъюнкции (относительно операндов):
3. Аксиомы переместительности операций дизъюнкции и конъюнкции (относительно операндов):
 4. Аксиомы одинаковых операндов:
4. Аксиомы одинаковых операндов:
 5. Аксиомы поглощения (множителем — множителя-суммы или слагаемым — слагаемого-произведения):
5. Аксиомы поглощения (множителем — множителя-суммы или слагаемым — слагаемого-произведения):
 6. Аксиомы распределения операции (дизъюнкции относительно конъюнкции и наоборот):
6. Аксиомы распределения операции (дизъюнкции относительно конъюнкции и наоборот):
 7. Аксиомы де Моргана (перенесения бинарной операции на операнды):
7. Аксиомы де Моргана (перенесения бинарной операции на операнды):
 8. Аксиомы нейтральности (взаимноинверсных множителей или слагаемых):
8. Аксиомы нейтральности (взаимноинверсных множителей или слагаемых):
 9. Аксиома существования единицы (истина, true, 1) и нуля (ложь, false, 0), причем,
9. Аксиома существования единицы (истина, true, 1) и нуля (ложь, false, 0), причем,
 Из этих аксиом следует ряд полезных соотношений, например,
Из этих аксиом следует ряд полезных соотношений, например,
 Три базовые операции алгебры предикатов определяются таблицей их значений, так как в алгебре предикатов из-за дискретности значений логических функций часто используется табличная форма задания функции. Булеву функцию n переменных можно полностью определить таблицей из 2n строк.
Итак, эти операции определяются совмещенной таблицей значений вида
Три базовые операции алгебры предикатов определяются таблицей их значений, так как в алгебре предикатов из-за дискретности значений логических функций часто используется табличная форма задания функции. Булеву функцию n переменных можно полностью определить таблицей из 2n строк.
Итак, эти операции определяются совмещенной таблицей значений вида





 . Эта таблица имеет вид
. Эта таблица имеет вид


 . Эта таблица имеет вид
. Эта таблица имеет вид


 . Имеем соотношение
. Имеем соотношение

 ;
; .
.
 Используя аксиомы алгебры предикатов, получаем равенства
Используя аксиомы алгебры предикатов, получаем равенства
 . Это выражение мы взяли из-за однозначности равенства 1 конъюнкции и неоднозначности (многовариантности) его равенства нулю. Упростим выражение:
. Это выражение мы взяли из-за однозначности равенства 1 конъюнкции и неоднозначности (многовариантности) его равенства нулю. Упростим выражение:
 , то заключаем, что автомобиль был черным "Бьюиком".
, то заключаем, что автомобиль был черным "Бьюиком". , то говорят, что высказывание y следует из высказывания x (или y – следствие x); если множество истинности Х высказывания х содержит множество истинности Y высказывания y, то высказывание x – условие, высказывание y – заключение, а само соотношение
, то говорят, что высказывание y следует из высказывания x (или y – следствие x); если множество истинности Х высказывания х содержит множество истинности Y высказывания y, то высказывание x – условие, высказывание y – заключение, а само соотношение 