Преимущества моделирования
Общая схема организации моделирования
Цели моделирования
Среди целей моделирования можно выделить следующие:
1. прогнозирование будущего состояния или поведения системы;
2. постановка экспериментов над моделью и анализ результатов применительно к моделируемой системе;
3. обучение и тренинг специалистов.
Построение математической модели начинается с выделения тех факторов, которые следует принять во внимание. Во многих физических задачах эти факторы связаны с условием равновесия сил, выполнением каких-либо законов сохранения и т.д. Поэтому построение модели является неизбежным компромиссом между учетом всех возможных факторов, играющих роль в данной задаче, и сохранением математической модели достаточно простой, чтобы ее можно было реализовать имеющимися в нашем распоряжении средствами. В классической науке рассматривались только очень простые модели явлений, т.к. решение приходилось находить вручную: либо аналитически, либо численно. Сегодня с увеличением мощности ЭВМ и развитием численных методов становится возможным работать со все более сложными моделями.
В окончательной формулировке математическая модель со всеми дополнительными условиями должна иметь единственное решение. Следующий шаг моделирования заключается в нахождении такого решения. Для проблем, которые существуют в настоящее время, редко удается получить решение в замкнутой форме; оно должно быть каким-то образом найдено приближенно (аппроксимировано). Методы аппроксимации решения дает численный анализ, его методы удобны для реализации на ЭВМ, сегодня они почти полностью вытеснили из практики другие методы решения.
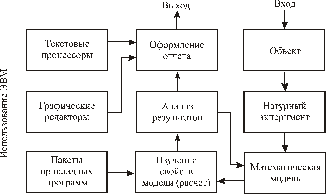
Рис. 2
Если можно находить решения модели, то следующим шагом является обоснование модели. Это доказательство того, что полученное решение является достаточно точным для тех целей, ради которых данная модель разрабатывалась.
Первая проверка правильности модели состоит в том, является ли найденное решение приемлемым. После того как большие ошибки исключены, что обычно бывает несложной задачей, начинается следующий этап проверки, состоящий в сравнении результатов расчетов с имеющимися экспериментальными данными или результатами наблюдений. Экспериментальные данные могут быть получены достаточно точно, физика эксперимента может существенно отличаться от математической модели. Требуется опыт и интуиция исследователя, чтобы сделать здравое заключение о том, достаточно ли хорошо согласуются расчеты математической модели с результатами наблюдений.
В начальной стадии исследования очень часто полученные результаты расчета не согласуются с результатами эксперимента или наблюдений, поэтому модель приходится модифицировать. Обычно это приводит к включению в нее некоторых дополнительных условий, которыми можно было бы пренебречь. Иногда требуется полный пересмотр модели и подход к изучению объекта с других позиций. Как только модель модифицирована, весь цикл начинается снова: новое численное решение, новое обоснование, дополнительные модификации и т.д.
Если в результате процесса обоснования и модификации модель будет признана адекватной, то она готова к использованию для предсказания, в чем и состоит основная цель ее построения.
Математическое моделирование в сравнении с натурным экспериментом обладает следующими преимуществами:
§ экономичностью – по сравнению с моделью практическая проверка реального объекта требует больших материальных и энергетических затрат;
§ возможностью моделирования гипотетических, т.е. нереализованных на практике объектов, например на этапе проектирования;
§ возможностью реализации опасных и трудновоспроизводимых в натуре режимов (аварий, катастроф и т.д.);
§ возможностью изучения процессов во времени;
§ возможностью прогнозирования и выявления общих закономерностей;
универсальностью технического и программного обеспечения проводимой работы (ПЭВМ, системы программирования, пакеты прикладных программ и т.д.).