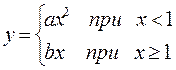Линейные и разветвляющиеся алгоритмы

Рис. 10.1. Алгоритмические структуры

Циклический- это алгоритм, в котором предусмотрено многократное выполнение одной и той же последовательности действий, называемых телом цикла. Цикл ­— повторение этой последовательности действий. При выполнении цикла изменяется значение некоторой переменной, которая называется параметром цикла. Когда параметр цикла достигнет заданного значения, цикл прекращается. Приведем общепринятые положения организации цикла:

1. Установить начальное значение параметра цикла;

2. Выполнить тело цикла;

3. Изменить параметр цикла;

4. Выполнить проверку: если параметр цикла не достиг заданного значения ­— возврат к пункту 2, иначе — к пункту 5;

5. Выход из цикла.

Проверка значения параметра цикла может выполняться в начале цикла (рис. 10.1,в). Такой алгоритм называют циклическим с предусловием или с защитой входа. Если проверка значения параметра цикла помещается в конце цикла (рис. 10.1,г), то такой тип алгоритма называют постусловием или свободным входом в цикл.

Существуют алгоритмы с заранее известным числом выполняемых циклов. Параметром цикла в таком случае является переменная, в которой накапливается количество выполняемых циклов - счетчик цикла. Когда будет выполнено заданное число циклов – осуществляется выход из цикла. Например, задачи обработки массивов данных сводятся к алгоритмам с заданным числом циклов.

Ряд задач сводятся к ЦА, в которых заранее неизвестно число выполняемых циклов. Например, определение суммы членов ряда с заданной точностью E , если задан общий член ряда а_n. Параметром цикла в данном случае является значение текущего члена ряда. Выход из цикла произойдет при a_n ≤ E. При уточнении корня алгебраического уравнения методом половинного деления параметром цикла является переменная z= b-a. Выход из цикла при выполнении условия z ≤ E.

При решении задач с использованием итерационных формул y_i+1 = f(y_i,x),выход из цикла осуществляется при выполнении условия | y_i+1 - y_i | <=E, где Е— заданная точность.

Циклические алгоритмы бывают простые (рис. 10.1,в,г) и сложные (на рис. 10.1,д представлен сложный циклический алгоритм без детализации начальной установки и изменения параметров внутреннего и внешнего циклов). Например, при решении задачи табулирования функции двух переменных Z=f(x,y) используется сложный циклический алгоритм, где параметром внутреннего цикла является х = x_нач., x_кон., dx_шаг., а параметром внешнего цикла y= y_нач.,y_кон.,dy_шаг.. К сложным циклическим алгоритмам сводятся задачи обработки элементов двумерных массивов и т.д.

Иерархические алгоритмы (рис. 10.1,е) используют подчиненные алгоритмы (подпрограммы). Алгоритм, из которого происходит обращение к подчиненному алгоритму, называют основным. Из основного алгоритма может происходить неограниченное число обращений к подчиненным алгоритмам.

Пример 10.1. Заданы значения переменных а, х. Составить алгоритм вычисления зависимости у=ах2

Пример 10.2. Заданы значения переменных а, в, х Составить алгоритм вычисления

 

 

 

 

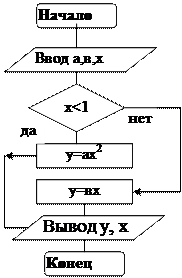Рис. 10.2. Линейный алгоритм Рис. 10.3. Разветвляющийся алгоритм