Представление чисел в форме с плавающей точкой

В общем случае любое число, представленное с плавающей точкой, может быть формализовано следующим образом

, где /q/ < 1.

Здесь – характеристика числа x (целая часть),

s – основание характеристики,

р – порядок,

q – мантисса числа x.

Порядок р может быть положительным или отрицательным целым числом. Он определяет положение точки в числе х.

Для двоичных чисел

, где /q/<1.

На рис.4.2 изображена форма представления чисел с плавающей точкой.

. . . . .

 

 

Рис. 4.2 Представление чисел с плавающей точкой.

 

– разряд для представления знака мантиссы (числа),

– знак порядка,

…– модуль порядка,

… – мантисса числа.

Например, порядок числа –5 представляется в виде 1000101.

– 5

Поскольку для порядка р, включая его знак, выделено семь разрядов, то порядок может быть любым целым числом от - 63 (1111111) до + 63 (0111111). Все числа, представляемые в форме с плавающей точкой, имеют нормализованный вид. Число называется нормализованным, если удовлетворяет условию

1 > /q/ >=

Для двоичных чисел s = 2. Проще говоря, нормализованное – это такое число, мантисса которого начинается со значащей цифры (не нуль). Двоичное число считается нормализованным, если в старшем разряде мантиссы стоит цифра 1. Наибольшее положительное нормализованное число будет =, наименьшее положительное число – . Число, представленное во всех разрядах разрядной сетки нулем, то есть имеющее положительную нулевую мантиссу и положительный нулевой порядок, называют и с т и н н ы м н у л е м. При фиксированном количестве разрядов мантиссы любая величина представляется в компьютере нормализованным числом с наиболее возможной точностью. В процессе вычислений может получаться ненормализованное число. В этом случае компьютер автоматически нормализует его, изменяя при этом порядок. Например, имеется ненормализованное число . После нормализации оно получит следующий вид . В ненормализованном числе четыре старших разряда представлены нулями. Чтобы их убрать, необходимо уменьшить порядок числа на четыре. То есть записать вместо 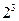характеристику . Нормализация невозможна при нулевой мантиссе. В этом случае процесс нормализации блокируется.

Известно также представление чисел в форме с плавающей точкой в системах счисления, основание которых равно положительной целой степени числа 2. То есть . Для восьмеричной системы счисления w=3. а для шестнадцатеричной – w =4. При этом порядок р представляется двоичным целым числом, а мантисса q- числом, в котором группы по w двоичных разрядов изображают цифры мантиссы с основанием системы счисления. Такой способ применим в восьмеричной и шестнадцатеричной системах счисления.

, где ( 1> /q/>=)

, где (1>/q/>=)

Использование недвоичных оснований несколько уменьшает точность вычислений, но расширяет диапазон представления чисел и ускоряет выполнение некоторых операций.

Арифметические действия над числами с плавающей точкой требуют, помимо операций над мантиссами, определенных операций над порядками (сравнение, вычитание и др.). Для упрощения операций над порядками их сводят к действиям над целыми положительными числами, применяя представление чисел с плавающей точкой со «смещенным порядком».

В случае представления чисел со смещенным порядком при его записи в память к его разряду р прибавляется целое число, называемое смещением и определяемое как , где k – число двоичных разрядов, используемых для модуля порядка. Смещенный порядок

всегда положительный. Для его представления требуется такое же количество разрядов, как для модуля и знака порядка р.