Двоичная арифметика
Двоичная система счисления
Системы счисления, используемые при работе с ЭВМ
Основание Р = 2. Алфавит включает две двоичные цифры: 0, 1. Любое число C = Cn Cn-1 …C1 C0 C-1 C-m есть сумма степеней числа Р = 2,
C = Cn× 2n +Cn-1× 2n-1 +…+C1× 21 +C0× 20 +C-1× 2-1 +…+C-m× 2-m
Пример 3.6.
101011,112 =1×25 + 0×24 + 1×23 + 0×22 +1×21 + 1×20 +1×2-1 + 1×2-2 = 32+8+2+1+0,5+0,25=43,7510.
Веса разрядов в двоичной системе счисления равны 1, 4, 8,16,... влево от запятой и 0,5; 0,25; 0,125; 0,625;... вправо от запятой.
При программировании иногда используется шестнадцатеричная система счисления. Для изображения цифр, больших 9, в шестнадцатеричной системе счисления применяются латинские буквы A, B, C, D, E, F. Изображения первых шестнадцати чисел в десятичной, двоичной и шестнадцатеричной системах счисления приведены в табл. 2.
Таблица кодов в различных системах счисления
Таблица 2
| Десятичная система | Двоичная система | Шестнад-цатеричная система | Десятичная система | Двоичная система | Шестнад-цатеричная система |
| А | |||||
| B | |||||
| C | |||||
| D | |||||
| E | |||||
| F |
Двоично-десятичная система счисления получила большое распространение в современных ЭВМ ввиду легкости перевода в десятичную систему и обратно. Она используется там, где основное внимание уделяется не простоте технического построения машины, а удобству работы пользователя. В этой системе счисления все десятичные цифры отдельно кодируются четырьмя двоичными цифрами.
Пример 3.7.
Десятичное число 9703 в двоично-десятичной системе выглядит так: 1001 0111 0000 0011.
Преимущество двоичной системы счисления над десятичной с точки зрения ЦВМ состоит в следующем:
- требуются элементы с двумя устойчивыми состояниями;
- существенно упрощаются арифметические операции;
- оборудования требуется в 1,5 раза меньше;
- позволяет применить аппарат математической логики для анализа и синтеза схем.
Недостатки двоичной системы счисления состоят в следующем:
- большая длина записи чисел;
- при вводе и выводе информации требуется перевод в десятичную систему счисления.
Рассмотрим, как выполняются основные действия в двоичной арифметике.
| Сложение | Вычитание | Вычитание | Деление |
| 0+0=0 | 0-0=0 | 0х0=0 | 0:1=0 |
| 0+1=1 | 1-0=1 | 0х1=0 | 1:1=1 |
| 1+0=1 | 1-1=0 | 1х0=0 | |
| 1+1=10 | 10-1=1 | 1х1=1 |
Правила арифметики во всех позиционных системах счисления одинаковы, т.е. сложение, умножение и вычитание начинают с младших разрядов, деление - со старших.
При сложении единица переноса складывается с цифрами соседнего старшего разряда. При вычитании единица заема старшего разряда дает две единицы в младшем соседнем разряде.
Пример 3.8
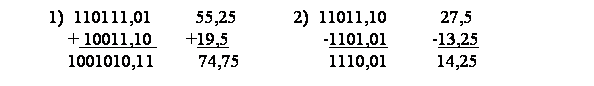
Умножение двоичных чисел аналогично умножению десятичных, но т.к. умножаем только на 0 и 1, то умножение сводится к операции сдвига и сложения.
Пример 3.9
