Основы рентгеноструктурного анализа

Основная формула дифракционной решетки (19.29) может быть использована не только для определения длины волны, но и для решения обратной задачи — нахождения постоянной дифрак­ционной решетки по известной длине волны. Такая скромная применительно к обычной дифракционной решетке задача подводит к практически важному вопросу — измерению параметров кристаллической решетки посредством дифракции рентгеновских лучей, что является содержанием рентгеноструктурного анализа.

Пусть совмещены две дифракционные решетки, штрихи которых перпендикулярны. Для решеток выполняются условия главных максимумов:

с₁ sin a₁ = ± k₁l, с₂ sin a₂ = ± k₂l (19.40)

Углы a₁и a₂отсчитываются во взаимно перпендикулярных направлениях. В этом случае на экране появится система пятен, каждому из которых соответствует пара значений k₁ и k₂ илиa₁и a₂. Таким образом, и здесь можно найти с₁ и с₂ по положению дифракционных пятен.

Усложняя задачу, логично считать, что дифракционная картина позволит измерить параметры и для трехмерной периодической структуры.

Естественной объемной периодической структурой являются кристаллы, крупные молекулы и т. п. Вторичные волны в кристалле возникают в результате взаимодействия первичных лучей с электронами атомов.

Для отчетливого наблюдения дифракционной картины должно выполняться определенное соотношение между длиной волны и параметром периодической структуры (см. § 19.5). Оптималь­ным условиям соответствует примерно одинаковый порядок этих величин. Учитывая, что расстояние между рассеивающими центрами (атомами) в кристалле (~10^-10 м) приблизительно равно длине волны рентгеновского излучения, можно считать, что крис­талл для этих лучей является трехмерной дифракционной решеткой.

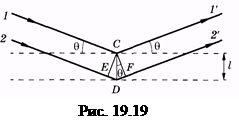На рис. 19.19 штриховыми линиями показаны две соседние кристаллографические плоскости. Взаимодействие рентгеновского излучения с атомами и возникновение вторичных волн можно рассматривать упрощенным методом как отражение от плоскостей. Пусть на кристалл под углом скольжения 9 падают рентгеновские лучи 1 и 2; 1¢и 2'— отраженные (вторичные) лучи, СЕ и CF — перпендикуляры к падающим и отраженным лучам соответственно. Разность хода отраженных лучей 1¢и 2'

d = ïDEï + ïDFï = 2l sinq, (19.41)

где l — межплоскостное расстояние.

Максимумы интерференции при отражении возникают в случае, когда разность хода равна целому числу длин волн:

2l sinq = kl; k = l,2, 3, ... (19.42)

Это условие Брэгга—Вульфа.

При падении монохроматического рентгеновского излучения на кристалл под разными углами наибольшее отражение (максимум) будет для углов, отвечающих условию (19.42). При регистрации под определенным углом скольжения пучка рентгеновского излучения со сплошным спектром максимум дифракции будет выполняться для длин волн, удовлетворяющих условию Брэгга—Вульфа.

 

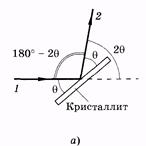
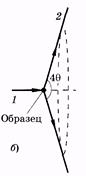
Рис. 19.20

П. Дебаем и П. Шеррером был предложен метод рентгено-структурного анализа, основанный на дифракции монохроматических рентгеновских лучей в поликристаллических телах (обычно спрессованные порошки). Среди множества кристаллитов всегда найдутся такие, для которых одинаковы l, q и k, причем эти величины соответствуют формуле Брэгга—Вульфа. Отраженный луч 2 (максимум) составит угол 2q с падающим рентгеновским лучом 1 (рис. 19.20, а). Так как условие (19.42) одинаково для многих кристаллов, по-разному ориентированных, то дифрагированные рентгеновские лучи образуют в пространстве конус, вершина которого лежит в исследуемом образце, а угол раствора равен 4q (рис. 19.20, б). Другой совокупности величии l, q и k, удовлетворяющих условию (19.42), будет соответствовать другой конус. На фотопленке рентгеновские лучи образуют рентгенограмму (дебае-грамму) в виде окружностей или дуг (рис. 19.21 а, б).

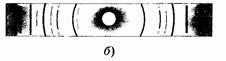
Рис. 19.21

 

Дифракцию рентгеновских лучей наблюдают также при рассея­нии их аморфными твердыми телами, жидкостями и газами. В этом случае на рентгенограмме получаются широкие и размытые кольца.

В настоящее время широко применяют рентгеноструктурный анализ биологических молекул и систем: на рис. 19.22 показаны рентгенограммы белков. Этим методом Дж. Уотсон и Ф. Крик установили структуру ДНК и были удостоены Нобелевской премии (1962). Использование дифракции рентгеновских лучей от кристаллов для исследования их спектрального состава относится к области рентгеновской спектроскопии.