Периодический взнос на накопление фонда. (Формирование фонда возмещения).

Периодический взнос в погашение кредита (взнос на амортизацию единицы).

Текущая стоимость аннуитета.

Текущая стоимость единицы.

Эта функция позволяет определить стоимость объекта недвижимости в текущий момент времени при известной будущей стоимости:

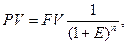(8)

При использовании эффективной процентной ставки (эффективной нормы дисконта) эта формула, соответственно, принимает вид:

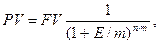(9)

Пример 5:

Какую сумму необходимо поместить на депозит сегодня под 10 % годовых, чтобы через 5 лет накопить 2 млн руб. для приобретения объекта недвижимости?

Решение:

Дано: PV = 2 млн руб., Е = 0,1; n = 5.

 

PV = 2(1 / (1 + 0,1)⁵ = 1,242 млн руб.

 

Эта функция позволяет определить текущую стоимость равномерных равновеликих поступлений денежных средств:

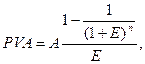(10)

где PVA – текущая стоимость аннуитета, руб.; A – сумма аннуитета, то есть сумма равновеликих равномерных поступлений денежных средств, руб.

Если Е установлена как годовая ставка доходности (норма дисконта), а поступления производятся чаще, чем раз в год (ежеквартально, ежемесячно и т.д.), то формула примет вид:

(11)

Пример 6:

Фирма сдает свободные площади в аренду. Определить текущую стоимость арендных площадей в течение 4 лет, если сдача в аренду торговых помещений может принести ежегодный доход в размере 670 тыс. руб. Ставка дисконта 9 % годовых.

Дано: A = 670; E = 0,09; n = 4.

 

тыс. руб.

Пример 7:

Инвестор рассматривает возможность вложения средств в объект недвижимости с целью получения дохода в виде арендной платы в течение пяти лет. Ежеквартальная сумма арендной платы, которая будет вноситься в конце каждого квартала, составит 500 тыс. руб. Какую максимальную цену целесообразно заплатить за объект сегодня при ставке дисконта 9% годовых.

Решение:

Дано: A = 500; E = 0,09; n = 5, m = 4.

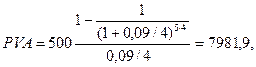тыс. руб.

 

Эта функция позволяет определить аннуитетные платежи в погашение текущей стоимости объекта или кредита:

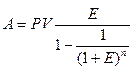. (12) (16)

При использовании эффективной ставки процента формула (12) примет, соответственно, вид:

 

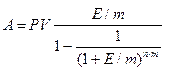(13)

.

Пример 8:

На приобретение объекта недвижимости выдан кредит в размере 2000 тыс. руб. сроком на 10 лет под 12 % годовых. Выплаты по кредиту осуществляются аннуитетным методом в конце каждого года. Определить, какую сумму необходимо выплачивать ежегодно в погашение кредита.

Решение:

Дано:

PV =2000 ; Е = 0,12; n = 5.

тыс.руб.

Пример 9:

На приобретение объекта недвижимости выдан кредит в размере 2000 тыс. руб. сроком на 10 лет под 12 % годовых. Выплаты по кредиту осуществляются аннуитетным методом в конце каждого месяца. Определить, какую сумму необходимо выплачивать ежемесячно в погашение кредита.

Решение:

Дано:

PV = 2000; Е = 0,12; n = 10; т = 12.

 

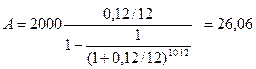тыс. руб.

В примере 9 можно видеть, что общая сумма выплат по кредиту при ежемесячном погашении будет значительно меньше, чем в случае ежегодного погашения, рассмотренного в примере 8 (26,06 × 12 × 10 = 3127,2, что меньше суммы выплат 336,8 × 10 = 3368).

 

С помощью этой функции определяются платежи для покрытия будущей стоимости объекта недвижимости:

. (15)

При использовании эффективной ставке процента формула примет следующий вид:

. (16)

 

Пример 10:

Для покупки жилого дома стоимостью 4000 тыс. руб. открыт накопительный жилищный счет с начислением по нему 10 % годовых. Какую сумму нужно вносить на счет ежегодно, чтобы накопить нужную сумму за пять лет?

Решение:

Дано:

FV = 2400; Е = 0,10; n = 5.

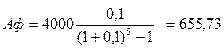тыс. руб.

Пример 11:

Для покупки жилого дома стоимостью 4000 тыс. руб. открыт накопительный жилищный счет с начислением по нему 10 % годовых. Какую сумму нужно вносить на счет ежемесячно, чтобы накопить нужную сумму за пять лет?

Решение:

Дано:

FV = 4000; Е = 0,10; n = 5; m = 12.

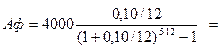51,65 тыс. руб.

Здесь также можно видеть, что чем чаще осуществляются взносы на накопительный счет, тем быстрее происходит накопление суммы и тем меньше суммарный годовой взнос (51,65 × 12 = 619,80 < 655,73).