Основные теоретические положения
ЛАБОРАТОРНАЯ РАБОТА № 13
Тема: Задача Коши для дифференциального уравнения п-го порядка
Цели работы:
1. Изучить способы представления исходных данных при решении задачи Коши для дифференциального уравнения порядка п с помощью программного продукта MathCAD.
2. Рассмотреть порядок решения задачи Коши для дифференциального уравнения порядка п при использовании MathCAD.
3. Научиться представлять результаты численного решения в графическом виде.
Основные теоретические положения
Определение.Дифференциальным уравнением порядка  называется уравнение, связывающее независимую переменную
называется уравнение, связывающее независимую переменную  , искомую функцию
, искомую функцию  и её производные до порядка
и её производные до порядка  включительно
включительно
 (1)
(1)
или
 . (2)
. (2)
Определение.Решением (частным решением) уравнения (1) или (2) на интервале  называется любая функция
называется любая функция  , которая, будучи подставлена в это уравнение вместе со своими производными
, которая, будучи подставлена в это уравнение вместе со своими производными  ,
,  , …,
, …,  обращает его в тождество относительно всех
обращает его в тождество относительно всех  . Уравнение
. Уравнение  , определяющее это решение как неявную функцию, называется интегралом (частным интегралом) дифференциального уравнения порядка
, определяющее это решение как неявную функцию, называется интегралом (частным интегралом) дифференциального уравнения порядка  .
.
Определение.Задачей Коши для дифференциального уравнения порядка  называется задача отыскания решения
называется задача отыскания решения  , удовлетворяющего заданным начальным условиям
, удовлетворяющего заданным начальным условиям
 . (3)
. (3)
Определение.Общим решением уравнения (1) или (2) называется такая функция  , которая при любых допустимых значениях параметров
, которая при любых допустимых значениях параметров  является решением этого дифференциального уравнения и для любой задачи Коши с начальными условиями (3) найдутся постоянные
является решением этого дифференциального уравнения и для любой задачи Коши с начальными условиями (3) найдутся постоянные  , определяемые системой уравнений
, определяемые системой уравнений
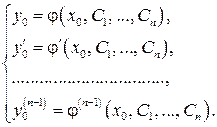
Определение.Уравнение  , определяющее общее решение как неявную функцию, называется общим интегралом дифференциального уравнения.
, определяющее общее решение как неявную функцию, называется общим интегралом дифференциального уравнения.
Теорема Коши. Если дифференциальное уравнение (2) таково, что функция  в некоторой области
в некоторой области  измерения свих аргументов непрерывна и имеет непрерывные частные производные
измерения свих аргументов непрерывна и имеет непрерывные частные производные  , то для любой точки
, то для любой точки  существует интервал
существует интервал  , на котором существует и притом единственное решение этого уравнения, удовлетворяющее начальным условиям (3).
, на котором существует и притом единственное решение этого уравнения, удовлетворяющее начальным условиям (3).