Методика и техника эксперимента

Справедливость соотношения неопределенностей можно проверить в опыте по дифракции фотонов на щели. Рассмотрим поток фотонов, который падает слева на непрозрачный экран М. В экране имеется щель шириной b (рис. 1). Энергия каждого фотона E. Как ранее было сказано, ми­крочастицы обладают волновыми свойствами. Поэтому поток фотонов с за­данной энергией можно рассматривать как пучок монохроматического света с длиной волны l или частотой n. Причем между введенными характе­ристиками фотона как частицы (Е, Р) и как волны (l, n) существует вполне определенная связь:

(4)

где с – скорость света в вакууме. Если на расстоянии L >> b от экрана М поместить второй непрозрачный экран N, то, как известно из курса оптики, на этом экране будет наблюдаться дифракционная картина, распределение освещенности для которой показано на рис. 1. Этому явлению мо­жно дать двоякое объяснение. С точки зрения волновой оптики явление ди­фракции объясняется перераспределением светового потока в результате суперпозиции волн от вторичных источников.

Рассмотрим теперь эту дифракционную картину с точки зрения пред­ставления о свете, как о совокупности световых квантов-фотонов. Если фотоны проходят через щель в экране М поодиночке, то каждый фотон попадает в определенную точку на эк­ране N. Предсказать, в какую именно точку попадает один отдель­но взятый фотон, принципиально не­возможно. Однако в совокупности большое число попавших на экран фотонов дает дифракционную картину. С точки зрения квантовой теории взаимодействие фотонов с веществом при прохождении света через прегра­ду приводит к перераспределению фотонов в пространстве и возникновению дифракционной картины на экране, расположенном на пути света, прошедшего через преграду (щель).

Рассмотрим, как происходит движение фотона в рассматриваемой сис­теме. Для прохождения фотона через щель нам точно известен импульс фо­тона:

(5)

направленный вдоль оси z, перпендикулярной экрану Ми N. Составляющая импульса фотона по оси Оxравна нулю (Dр_х =0), т.е. извест­на точно, но зато совершенно не определена координата фотона х. При прохождении фотона через щель в экране М ширина щели b бу­дет служить мерой неопределенности Dx значения координаты фотона x. Далее, по корпускулярным представлениям возникновение на экране диф­ракционной картины следует истолковать в том смысле, что каждый отде­льно взятый фотон, пройдя через щель, отклоняется либо вверх, либо вниз. Но для этого фотон должен приобрести составляющую импульса DР_x, перпендикулярную направлению первоначального движения. Величина полно­го импульса фотона Р как следует из (5), не меняется, т.к. не меняется длина волны.

Возникает вопрос: в результате чего фотоны приобретают составляю­щую импульса, перпендикулярную направлению первоначального движения? Ответ может быть только один: в результате «взаимодействия» со щелью в экране М, поскольку никаким другим воздействиям фотоны не подверга­лись. А в чем же заключается «взаимодействие» фотона с щелью? Ясно, что это не есть взаимодействие в классическом смысле, так как размеры щели много больше размеров фотона. В такой ситуации классическая час­тица просто «не заметила» бы щели на своем пути и продолжала бы двига­ться в прежнем направлении. Квантовая же частица, в силу уже упомя­нутых выше необычных своих свойств, «чувствует» любые изменения окружающего ее пространства. Поэтому стоило измениться пространству, окружающему рассматриваемые фотоны (появилась пусть и широкая, но щель – пространство вдоль оси Ох«сжалось»), как они тут же «отреагирова­ли» Причем чем уже щель, через которую должны проходить фотоны, тем более вероятным становится их отклонение на большие углы от направле­ния первоначального движения.

 

Оценим произведение Dх×DР_х.

Как было отмечено выше, Dх = b.Определить значение состав­ляющей DР_х каждого фотона невозможно, так как принципиально нево­зможно предсказать, куда пойдет каждый отдельный фотон после прохождения щели, но мы знаем, что большая часть фотонов попадает в область главного максимума. (Поскольку освещенность в максимумах дифракционной картины спадает в пропорции 1000 : 47 : 17, вероятностью попадания фотонов в побочные максимумы можно пренебречь). Поэтому, как видно из рис. 1, мера неопределенности компонента импульса Р_х после прохождения фотона через щель равна

DР_х = Р×sinj, (6)

где j - угол дифракции, характеризующий направление на первый мини­мум дифракционной картины. Теперь имеем Dx×DP_x =bP×sin j или с учетом (4)

Dx×DP_x (7)

Из выражения (7) следует, что возможно провести экспериментально оцен­ку соотношения неопределенностей для фотонов с известной энергией.

Для экспериментальной проверки соотношения неопределенностей собирается установка по схеме, изображенной на рис. 2. Установка состоит из полупроводникового лазера (1), рамки с регулируемой щелью (2), укрепленной в держателе, однокоординатного столика с закрепленным на нем окуляр-микрометром и экрана (3). Длина волны излучений l = 0,643 мкм. Все детали

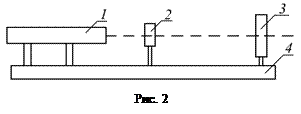установки располагаются на оптическом рельсе (4).