ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФКДЕРАЦИИ

Государственное образовательное учреждение высшего профессионального образования

«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ

ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Институт Неразрушающего контроля

 

Кафедра Промышленной и

медицинской электроники

 

 

Лабораторная работа № 3-17.
«ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА СООТНОШЕНИЯ НЕОПРЕДЕЛЕННОСТЕЙ ДЛЯ ФОТОНОВ»

 

 

Работу выполнили

Студенты группы 1Д10______________________Васнев Н.А.
______________________Мартынов Ю.М.

(дата, подпись)

Проверил преподаватель_____________________ Краснов Д.Н.

(дата, подпись)

 

Томск-2012

Цель работы: сформулировать гипотезу исследования, проверить соотношение неопределенностей для фотонов.

Приборы и принадлежности: полупроводниковый лазер, щель раздвижная, окуляр-микрометр, однокоординатный столик для крепления и перемещения окуляр-микрометра, экран, оптический рельс.

 

 

Краткое теоретическое введение:

Движение частиц в области микромира описывается квантовой или волновой механикой. Одним из фундаментальных положений квантовой механики является принцип неопределенностей, сформулированный В. Гейзенбергом в 1927 г. О том, каково его значение, можно судить, исходя из того факта, что всего одного из соотношений неопределенностей достаточно, чтобы объяснить целый ряд закономерностей в атомной и ядерной физике. В частности, он позволяет объяснить тот факт, что электрон не падает на «дно» атома, а также оценить размеры простейшего атома и минимальную возможную энергию электрона в таком атоме. Соотношения неопределен­ностей указывают, в каком случае можно пользоваться понятиями классической механики применительно к микрочастицам, в частности, с какой степенью точности можно говорить о траекториях микрочастиц.

В классической механике для описания движения частиц применимо такое понятие, как траектория. При этом частице в каждый момент времени приписываются определенная координата хи определенное значение про­екции импульса Р_х. Координата хзадает положение частицы, а импульс Р_хуказывает, как изменяется это положение в течение бесконечно малого интервала времени:

х + dx = x + 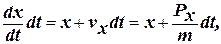(1)

где m – масса частицы; v_x – проекция скорости частицы на ось x. На смену классической механики для описания движения микрочастиц пришла квантовая механика. Это обусловлено двойственной природой микрочас­тиц. Всякий микрообъект (молекула, атом, электрон, фотон и т.д.) обла­дает свойствами и волны, и частицы. В то же время микрочастицы не ведут себя ни как волны, ни как частицы. Отличие микрочастицы от волны заключается в том, что она всегда обнаруживается как неделимое целое. Никому еще не удавалось наблюдать, например, пол-электрона. Волну же можно разделить на части, например направить ее на полупрозрачное зеркало и воспринимать затем каждую часть в отдельности. Своеобразие свойств микрочастиц проявляется в том, что не для всех переменных получаются при измерениях определенные значения. Неопределенности значений х и Рудовлетворяют соотношению

Dх×DР_х ≥ h, (2)

где Dх, DР_х–неопределенности значений х и Р_х, соответственно; h = h / 2p.

Из (2) следует, что чем меньше неоп­ределенность одной из переменных (х или Р_х), тем больше неопределен­ность другой. Возможно такое состояние микрочастицы, в котором одна из перечисленных переменных имеет точное значение (ее неопределенность равна нулю), другая переменная при этом оказывается совершенно неопределенной (ее неопределенность равна бесконечности).

Соотношение, аналогичное (2), имеет место для у и Р_у, для zи Р_z, а также для ряда других пар величин, которые в классической меха­нике называются канонически сопряженными. Обозначив канонически сопряженные величины буквами Аи В, можно написать

DA×DB ≥ 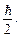(3)

Соотношение (3) называется соотношением неопределенностей для величин А и В.

Принцип неопределенностей Гейзенберга: произведение неопределен­ностей значений двух канонически сопряженных переменных не может быть по порядку величины меньше постоянной Планка h.

Соотношение неопределенностей – фундаментальный закон природы, ко­торый не выводится, не доказывается теоретически, а справедливость его доказывается экспериментально. Нужно заметить следующее: неправильно было бы величины DAи DB понимать только как неточности измерения ве­личин А и В, поскольку сам термин «неточность» как бы предполагает, что существуют и более точные значения Аи В (например, координаты и импу­льса), но только они почему-то не могут быть измерены. На самом деле невозможность такого измерения есть следствие того, что микрочастица по своей природе не имеет одновременно точного значения координаты и импульса. Иначе говоря, эта невозможность есть следствие корпускулярно-волновой природы микрочастицы.